Two identical containers A and B are filled with two different liquids of equal masses. The level of the liquid in container A is found to be one-fourth of the level of the liquid in container B. What is the ratio of thedensity of two liquids? If the density of he liquid in the container A is 2 " g " $c m^{- 3}$ , then find the density of the mixture of the two liquids.

Video Solution

Text Solution

Verified by Experts

Mass of liquid A, $(m_{A})$ = mass of liquid B, $(m_{B})$
Volume = $a r e a \times h e i g h t$
Area of cross section of A = Area cross section of B
Height of liquid column A = $\frac{1}{4} \times$ " height " of liquid column A = $\frac{1}{4} (Volume of B) D e n s i t y o f$ "mass/volume"(density " of " A)/(density " of " B) = m_(A)/V_(A)xx V_(B)/m_(B)=V_(B)/V_(B)=4/1=4 :1 $ I f d e n s i t y o f A i s 2 g$ cm^(-3) $, t h e n d e n s i t y o f B = g$ cm^(-3) $= 0.5 g$ cm^(-3) $ D e n s i t y o f m i x t u r e =$ "mass of mixture"/"volume of mixture" $$ (m_(A)+m_(B))/(v_(A)+v_(B))=(m_(A)=m_(A))/(v_(A)=4v_(A)) ( :. m_(B) = m_(A) and v_(B)= 4v_(A)) $$ (2m_(A))/(5v_(A)) = (2xx d_(A)xx v_(A))/(5V_(A) $$ (2xx2)/5=4/5=0.8 " g "cm^(-3)

Updated on:21/07/2023

The pressure exerted by a liquid column at the bottom of the liquid container is
Adoes not depend on the area of cross-section of container.
Bdependent on the density of the liquid.
Cequal in all directions.
DAll the above are true
The liquid inside the container has density $ρ$ . Choose the correct option.

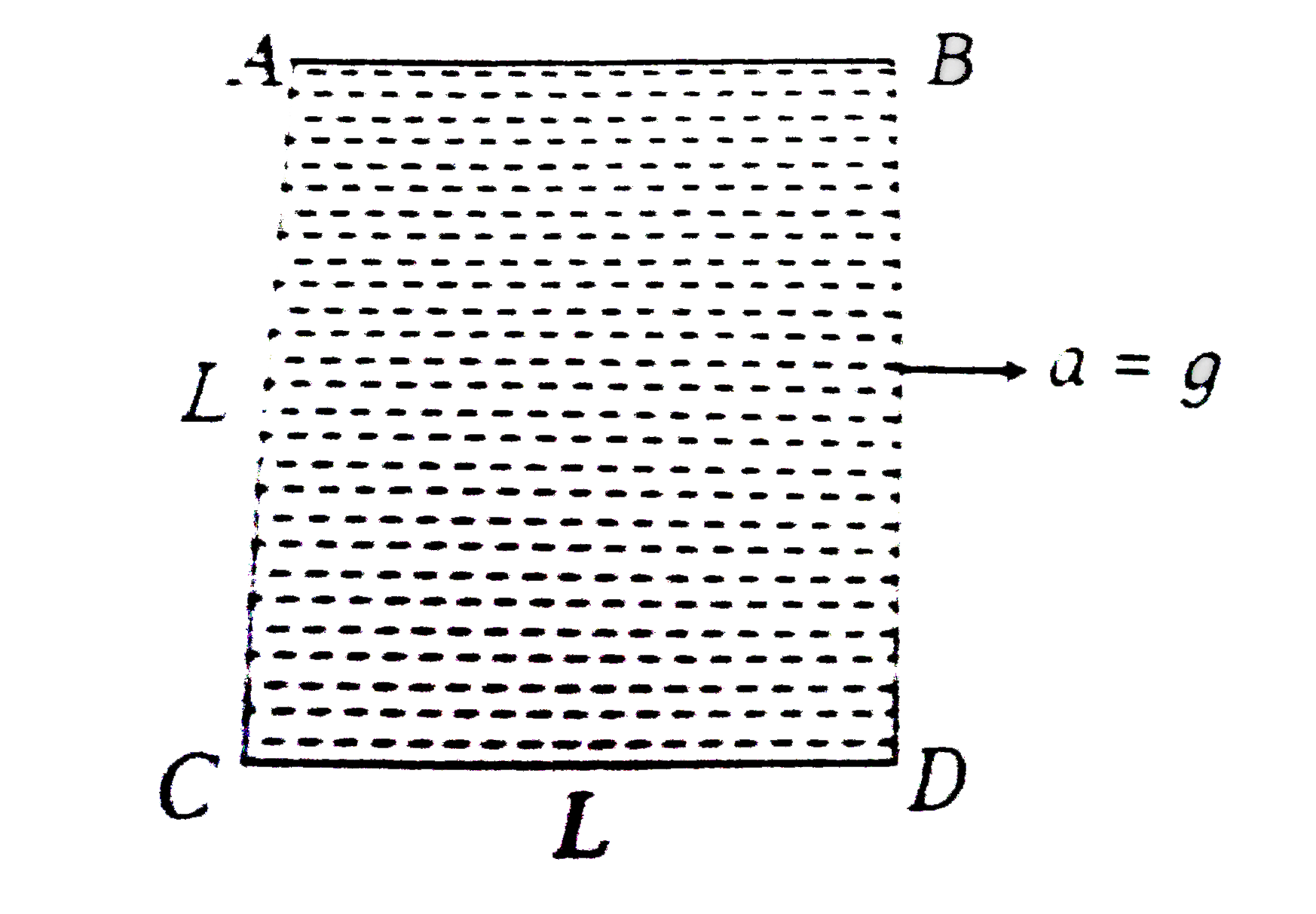A $p_{A} - p_{C} = 2 ρ g L$
B $p_{C} - p_{B} = \sqrt{2} ρ g L$
C $p_{C} - p_{D} = ρ g L$
D $p_{A} - p_{D} = 0 ρ g L$
A container filled with a liquid A is floating on the surface of another liquid 'B' as shown in the figure, then volume of the liquid displaced by the container

Ais equal to the volume of the liquid A.
Bis greater than the volume of the liquid A.
Cis less than the volume of the liquid A.
DCannot be determined