Two identical containers of same emissivity containing liquids A & B at same temperature of 60∘ initially and densitiy ρA and ρB respectively. Where ρA lt ρB. Which plot best represents the temperature varitation of both with time? Given (SA=1000Jkg−K,SB=2000Jkg−K)
Step by step video solution for Two identical containers of same emissivity containing liquids A & B at same temperature of 60^(@) initially and densitiy rhoA and rhoB respectively. Where rhoA lt rhoB. Which plot best represents the temperature varitation of both with time? Given (S_(A) = 1000(J)/(kg - K), S_(B) = 2000(J)/(kg- K)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Two metallic spheres S1andS2 are made of the same material and have got identical surface finish. The mass of S1 is thrice that of S2. Both the spheres are heated to the same high temperature and placed in the same room having lower temperature but are thermally insulated from each other. the ratio of the initial rate of cooling of S1 to that of S2 is
(a)13(b)1√3(c)√31(d)(13)13
View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
If vapours are collected in a container of volume 8.21L maintained at 3T/2K, where T=50K, then the ratio of initial rate of effusion of gases A and B is given as
View SolutionTwo closed Identical conducting containers are found in the laboratory of an old scientist. For the verification of the gas some experiments are performed on the two boxes and the results are noted.
_E01_208_Q01.png)
Experiment 1
When the two containers are weighed WA=225g,WB=160g and mass of evacuated container WC=100g.
Experiment 2.
when the two containers are given same amount of heat same temperature rise is recorded . The pressure change found are ΔPA=2.5atm. ΔPB=1.5atm
Identify the type of gas filled in container A and B respectively
_E01_208_Q01.png)
View SolutionFigure shows a large tank of water at a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1(<θ0). A metal rod of length L, area of cross section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0) . Specific heat capacity of water is s and all other heat capacities are negligible.

View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
Vapours of A and B are passed into a container of volume 8.21L, maintained at 2TK, where T=50K and after 5min, moles of B=8/3. The pressure developed into the cotainer after two half lives is
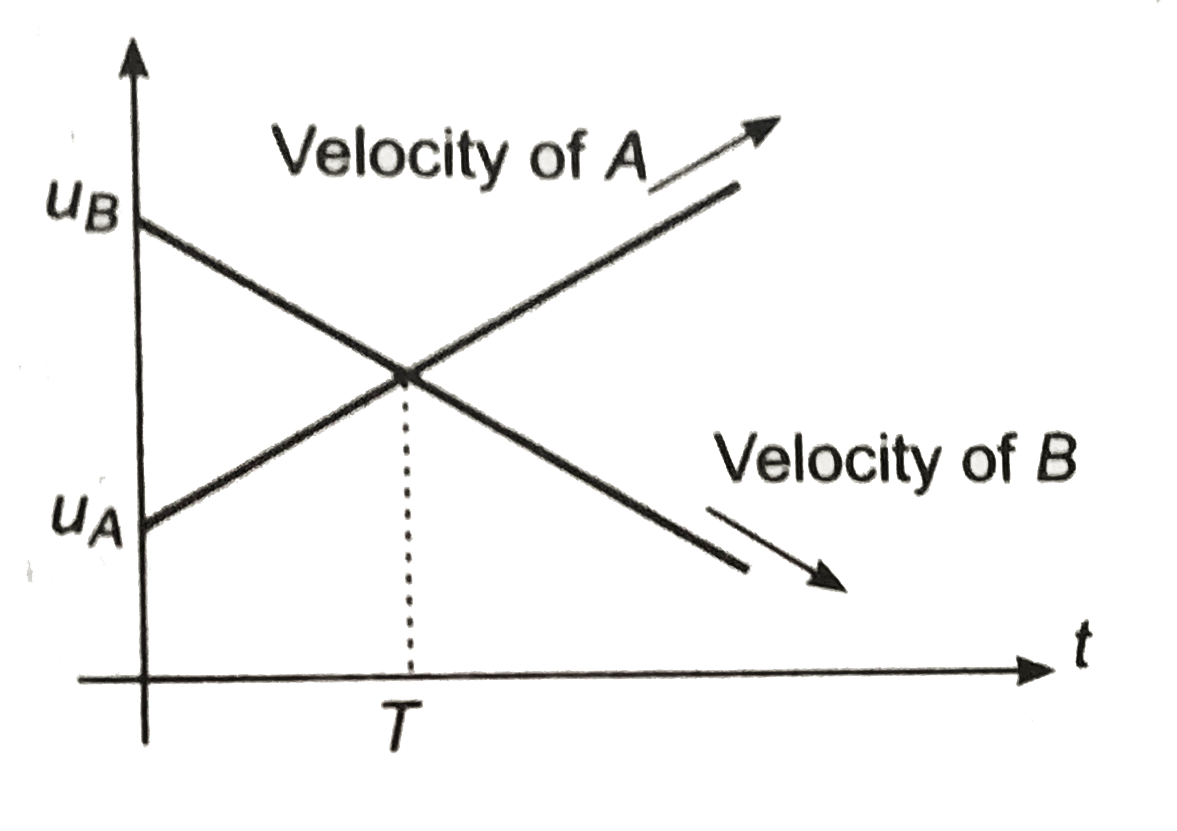
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
7. After 10 s of the start of motion of both objects A and B, find the value of velocity of A if uA=6ms−1,uB=12ms−1 and at T velocity of A is 8ms−1andT=4s
View SolutionAn adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U=1.5nRT) and the part on the right contains two moles of the same gas. initially, the pressure on each side is p. the system is left for sufficient time so that a steady state is reached. find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c ) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionA calorimeter of mass 0.2kg and specific heat 900J/kg−K. Containing 0.5kg of a liquid of specific heat 2400J/kg−K. Its temperature falls from 60∘C to 55∘C in one minute. Find the rate of cooling.
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution
