Question

Two identical loudspeakers are driven in phase by a common oscillator at $800Hz$ and face each other at a distance of $1.25m$. Locate the points along the line joining the two speakers where relative minimum of sound pressure amplitude would be expected. ( Use $v=343m/s$.)

Explanation

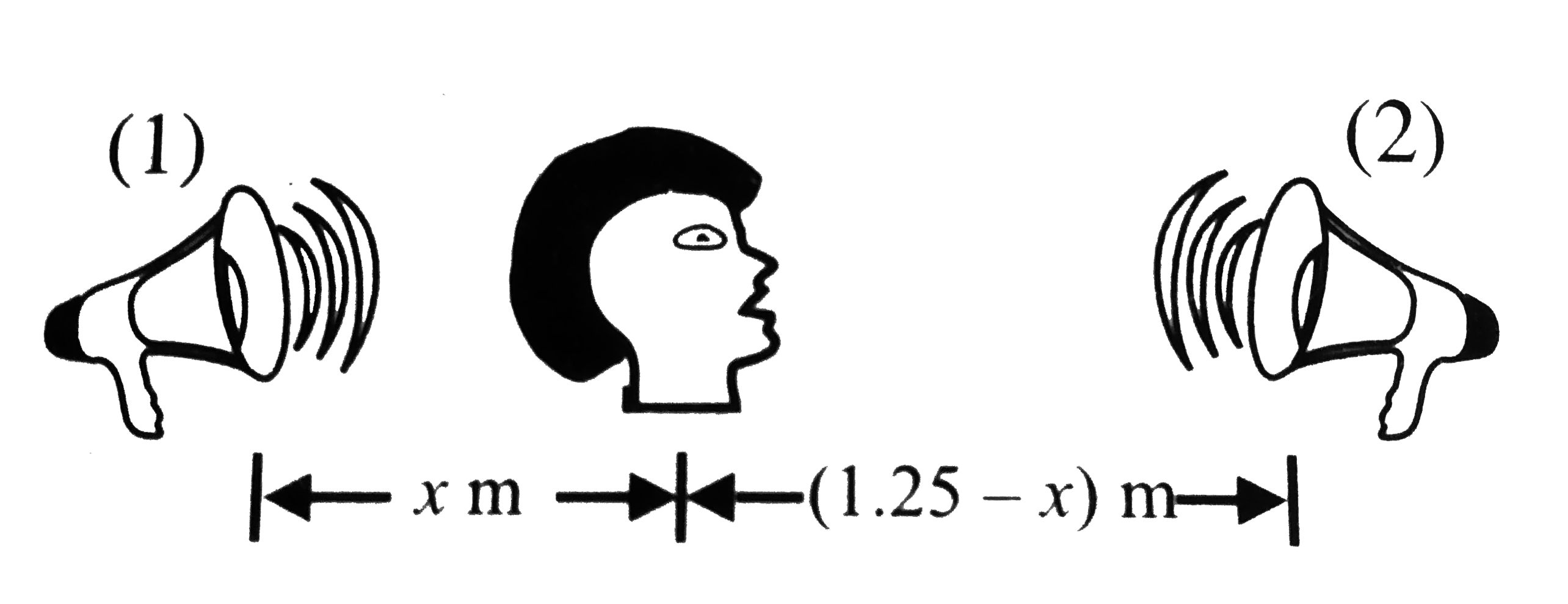
Two identical waves moving in opposite directions constitute a standing wave .We must find the nodes.
The wavelength is
` lambda = (v)/(f) = ( 343 m//s)/( 800 Hz) = 0.429 m`
The two waves moving in opposite directions along the line between the two speakers will add to produce a standing wave within this distance between nodes.
Distance node to node ` = lambda//2 = 0.214 m`
Because the speakers vibrate in phase , air compressions from each will simultaneously reach the point halfway between the speakers , to produce antinode of pressure here . A node of pressure will be located at this distance on either side of the midpoint.
Distance node to antinode ` = lambda //4 = 0.107 m`
Therefore nodes of sound pressure will appear at these distances from either speaker.
`[ 1//2 ( 1.25 m) + 0.107 m = 0.732 m`
and `1//2 ( 1.25 m) - 0.107 m = 0.518 m ]`
The standing wave contains a chain of equally spaced nodes at distances from either of the speakers
`0.732 m + 0.214 m = 0.946 m`
` 0.947 m + 0.214 m = 1.16 m`
also at ` 0.518 m - 0.214 m = 0.303 m`
`0.303 m - 0.214 m = 0.089 m`
The standing wave exists only along the line segment between the speakers . No nodes or antinodes appear at distances greater than `1.252 m` or less than `0`, because waves add to gives standing wave only if they are travelling in opposite directions and not in the same direction . Thus , the distances from either of the speakers to the nodes of pressure between the speakers are `0.089 m , 0.303 m , 0.732 m , 0.946 m and 1.16 m`