Two identical metal balls one at T1=300K and the other T2=600K are kept at a distance of 1m in vacuum. Will the temperatures equalize by radiation? Will the rate of heat gained by the colder sphere be proportional to T42−T41 as may be expected from the Stefan's law ?
To solve the problem, we need to analyze the situation of two identical metal balls at different temperatures placed in a vacuum and determine if their temperatures will equalize through radiation, and if the rate of heat gained by the colder ball is proportional to the difference in the fourth power of their temperatures.
1. Understanding the System:
- We have two identical metal balls, Ball A at T1=300K and Ball B at T2=600K.
- They are separated by a distance of 1 meter in a vacuum.
2. Radiation Emission:
- Both balls will emit thermal radiation according to the Stefan-Boltzmann law, which states that the power radiated by a black body is proportional to the fourth power of its absolute temperature:
P=σAT4
- Here, σ is the Stefan-Boltzmann constant, A is the surface area of the balls, and T is the temperature in Kelvin.
3. Heat Exchange Between the Balls:
- Ball B (at 600 K) will emit more radiation than Ball A (at 300 K) because it is at a higher temperature.
- The colder ball (Ball A) will absorb some of the radiation emitted by the hotter ball (Ball B).
4. Will the Temperatures Equalize?:
- Yes, the temperatures of the two balls will eventually equalize due to the continuous exchange of thermal radiation.
- As Ball A absorbs radiation from Ball B, its temperature will increase, while Ball B will lose some energy and its temperature will decrease.
- This process continues until thermal equilibrium is reached, meaning both balls will have the same temperature.
5. Rate of Heat Gain:
- The rate of heat gained by the colder sphere (Ball A) can be expressed as:
dQdt=σA(T42−T41)
- This shows that the rate of heat gained by Ball A is indeed proportional to the difference in the fourth powers of their temperatures, T42−T41.
6. Conclusion:
- The temperatures of the two balls will equalize through radiation.
- The rate of heat gained by the colder sphere is proportional to T42−T41, consistent with Stefan's law.
- We have two identical metal balls, Ball A at T1=300K and Ball B at T2=600K.
- They are separated by a distance of 1 meter in a vacuum.
- Both balls will emit thermal radiation according to the Stefan-Boltzmann law, which states that the power radiated by a black body is proportional to the fourth power of its absolute temperature:
P=σAT4
- Here, σ is the Stefan-Boltzmann constant, A is the surface area of the balls, and T is the temperature in Kelvin.
- Ball B (at 600 K) will emit more radiation than Ball A (at 300 K) because it is at a higher temperature.
- The colder ball (Ball A) will absorb some of the radiation emitted by the hotter ball (Ball B).
- Yes, the temperatures of the two balls will eventually equalize due to the continuous exchange of thermal radiation.
- As Ball A absorbs radiation from Ball B, its temperature will increase, while Ball B will lose some energy and its temperature will decrease.
- This process continues until thermal equilibrium is reached, meaning both balls will have the same temperature.
- The rate of heat gained by the colder sphere (Ball A) can be expressed as:
dQdt=σA(T42−T41)
- This shows that the rate of heat gained by Ball A is indeed proportional to the difference in the fourth powers of their temperatures, T42−T41.
- The temperatures of the two balls will equalize through radiation.
- The rate of heat gained by the colder sphere is proportional to T42−T41, consistent with Stefan's law.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE55videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 26videos
HEAT AND TEMPERATURE
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer4videos
INTRODUCTION TO PHYSICS
Similar Questions
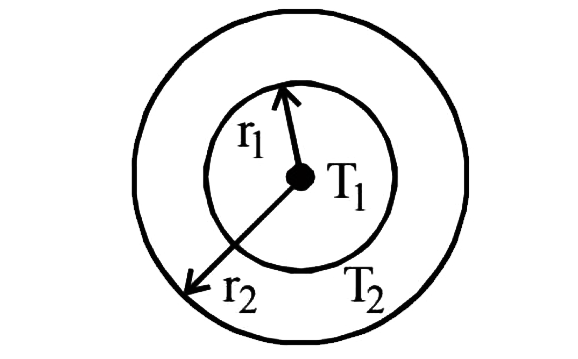
The figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
 View Solution
View SolutionA black body, at temperature T K emits radiation at the rate of 81 W/m2. It the temperature falls to t=T/3 K. then the new rate of thermal radiation will be
View Solution
Knowledge Check
- Question 1 - Select One
Two walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2 - Question 2 - Select One
Assertion : Current versus potential difference (i-V) graph for a conductor at two different temperatures T1 and T2 is shown in figure. Hence T1>T2.

Reason : Resistance of a conductor increases with rise in temperature.Acos2θBsin2θCcot2θDtan2θ
A solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
View SolutionThe figure shows a system of two concentric spheres of radii r 1 and r 2 and kept at temperature T 1 and T 2 , respectively. The radial rate of flow of heat in a substance between the two concentric spheres, is proportional to:
View SolutionTwo conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View SolutionTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionIf K1= Rate constant at temperature T1 and k2 rate constant at temperature T2 for a first order reaction, then which of the following relation is correct ?
View Solution

