Two closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
2P1T2T1+T2
2P1T1+T2
2P1T2T1+T2
none of these
The correct Answer is:C
To solve the problem step by step, we will use the Ideal Gas Law and the concept of conservation of moles. Here’s how we can derive the final pressure in the two connected vessels:
Step 1: Understand the Initial Conditions
Initially, both vessels have the same pressure P1 and temperature T1. The volume of each vessel is V.
Step 2: Write the Expression for Initial Moles
Using the Ideal Gas Law, the number of moles n in each vessel can be expressed as:
n=PVRT
For both vessels at the initial state:
- For vessel 1:
n1=P1VRT1
- For vessel 2:
n2=P1VRT1
Thus, the total initial moles ninitial is:
ninitial=n1+n2=P1VRT1+P1VRT1=2P1VRT1
Step 3: Write the Expression for Final Moles
After connecting the vessels, one vessel is maintained at temperature T1 and the other at T2. Let the final pressure in both vessels be P. The number of moles in each vessel now is:
- For vessel 1 (at T1):
n′1=PVRT1
- For vessel 2 (at T2):
n′2=PVRT2
Thus, the total final moles nfinal is:
nfinal=n′1+n′2=PVRT1+PVRT2=PV(1RT1+1RT2)
Step 4: Equate Initial and Final Moles
Since the number of moles is conserved, we can set the initial moles equal to the final moles:
2P1VRT1=PV(1RT1+1RT2)
Step 5: Simplify the Equation
Cancel V from both sides (assuming V≠0):
2P1RT1=P(1RT1+1RT2)
Now, multiply both sides by RT1RT2:
2P1RT2=P(RT2+RT1)
Step 6: Solve for P
Rearranging gives:
P=2P1RT2RT1+RT2
Since R is a constant, it cancels out:
P=2P1T2T1+T2
Final Result
The final pressure P in both vessels is:
P=2P1T2T1+T2
Initially, both vessels have the same pressure P1 and temperature T1. The volume of each vessel is V.
Using the Ideal Gas Law, the number of moles n in each vessel can be expressed as:
n=PVRT
For both vessels at the initial state:
- For vessel 1:
n1=P1VRT1
- For vessel 2:
n2=P1VRT1
Thus, the total initial moles ninitial is:
ninitial=n1+n2=P1VRT1+P1VRT1=2P1VRT1
After connecting the vessels, one vessel is maintained at temperature T1 and the other at T2. Let the final pressure in both vessels be P. The number of moles in each vessel now is:
- For vessel 1 (at T1):
n′1=PVRT1
- For vessel 2 (at T2):
n′2=PVRT2
Thus, the total final moles nfinal is:
nfinal=n′1+n′2=PVRT1+PVRT2=PV(1RT1+1RT2)
Since the number of moles is conserved, we can set the initial moles equal to the final moles:
2P1VRT1=PV(1RT1+1RT2)
Cancel V from both sides (assuming V≠0):
2P1RT1=P(1RT1+1RT2)
Now, multiply both sides by RT1RT2:
2P1RT2=P(RT2+RT1)
Rearranging gives:
P=2P1RT2RT1+RT2
Since R is a constant, it cancels out:
P=2P1T2T1+T2
The final pressure P in both vessels is:
P=2P1T2T1+T2
Topper's Solved these Questions
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - EFFICIENT
45 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IMPECCABLE
50 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IMPECCABLE
50 Videos
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - IN - CHAPTER EXERCISE - H
8 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IN-CHAPTER EXERCISE-I
10 Videos
Similar Questions
Two closed vessel A and B of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a naroow open tube. If th temperature of one is now maintained at T1 and other at T2 (wehre T1>T2 ) then that what will be the final pressure ?
View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below . The temperature of one of the bulbs is then raised to T2 . the final pressure Pf is
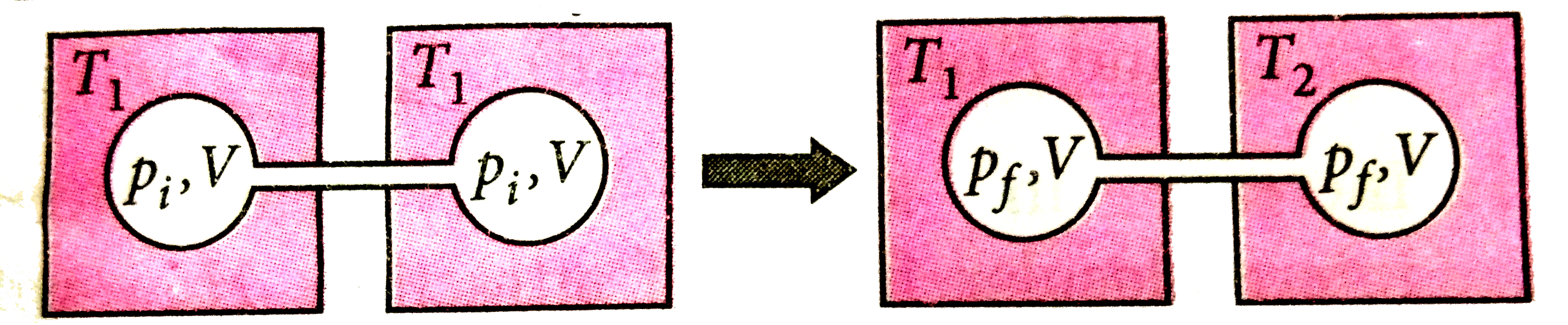
View SolutionA vessel of volume V is divided into two parts by a partition. The pressure of the gas in one part is p1 and that in the other part is p2. If the partition is removed find the pressure of the gas in the vessel.
View SolutionA closed vessel A having volume V contains N2 at pressure P and temperature T. another closed vessel B having the same volume V contains. He at the same pressure P. but temperature 2T. The ratio of masses of N2 and He in the vesses A and B is
View SolutionEqual masses of air are sealed in two vessels, one if volume V0and the other of volume 2V0.If the first vessel is maintained at a temperature 300K and the other at 600K, find the ratio of the pressures in the two vessels.
View SolutionEqual masses of air are sealed in two vessels, one of volume V0 and the other of volume 2V0. If the first vessel is maintained at a temperature 300K and the other at 600K, find the ratio of the pressures in the two vessels.
View SolutionTwo identical containers joned by a small pipe initially contain the same gas at pressue po and abosolute temperature To. One container is now mantained at the same temperature while the other is heated to 2T0. The commmon pressure of the gases will be
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
View SolutionGaseous system is placed with pressure P1, volume V1 and temperature T1, it has undergone thermodynamic changes where temperature is remaining constant, it is
View Solution
