Two identical sources each of intensity I0 have a separation d=λ/8, where λ is the wavelength of the waves emitted by either source. The phase difference of the sources is π/4 The intensity distribution I(θ) in the radiation field as a function of θ Which specifies the direction from the sources to the distant observation point P is given by
I(θ)=I0cos2θ
I(θ)=I04cos2(πθ8)
I(θ)=4I0cos2[π8(sinθ+1)]
I(θ)=I0sin2θ
The correct Answer is:c
Δx=sinθ=λ8sinθ
Δϕ= phase difference at P
Δϕ=2πλ(Δx)+Δϕ'=2πλ(λ8sinθ)+π4
I(θ)=4I0cos2(Δϕ2)
=4I0cos2[π8(1+sinθ)]

Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
The intensities of two light sources are I and 91 .If the phase difference between the waves is pi then resultant intensity will be :-
View SolutionTwo sources of intensity I and 4 are used in an interference experiment. Find the intensity at point where the waves from two sources superimpose with a phase difference (i) zero (ii) π/2 and (iii) π.
View Solution
Knowledge Check
Two identical radiators have a separation of d=λ/4 where λ is the wavelength of the waves emitted by either source. The initial phase difference between the sources is λ/4. Then the intensity on the screen at a distant point situated at an angle θ=30∘ from the radiators is (here I0 is intensity at that point due to one radiator alone)
A(a) I0B(b) 2I0C(c) 3I0D(d) 4I0Two sources of intensity 2I and 8I are used in an interference experiment. The intensity at a point where the waves from two sources superimpose with a phase difference of (a) zero (b) π/2and(c)π is
A18I,10I,2IB5I,4I,IC2I,I,I2D2I,10I,18IIn Young's double slit experiment, the constant phase difference between two source is π2 . The intensity at a point equidistant from theslits in terms of maximum intensity I0 is
AI0BI0/2C3I0/4D3I0
Two light sources with intensity I0 each interfere in a medium where phase difference between them us π2. Resultant intensity at the point would be.
View SolutionWaves from two sources of intensities I and 3I are used in an interference experiment. Calculate the intensity at point where the waves superimpose with a phase difference of (i)π/2and(ii)π.
View SolutionTwo coherent sources each emitting light of intensity I0 Interfere, in a medium at a point, where phase different between them is 2π3. Then, the resultant intensity at that point would be.
View Solution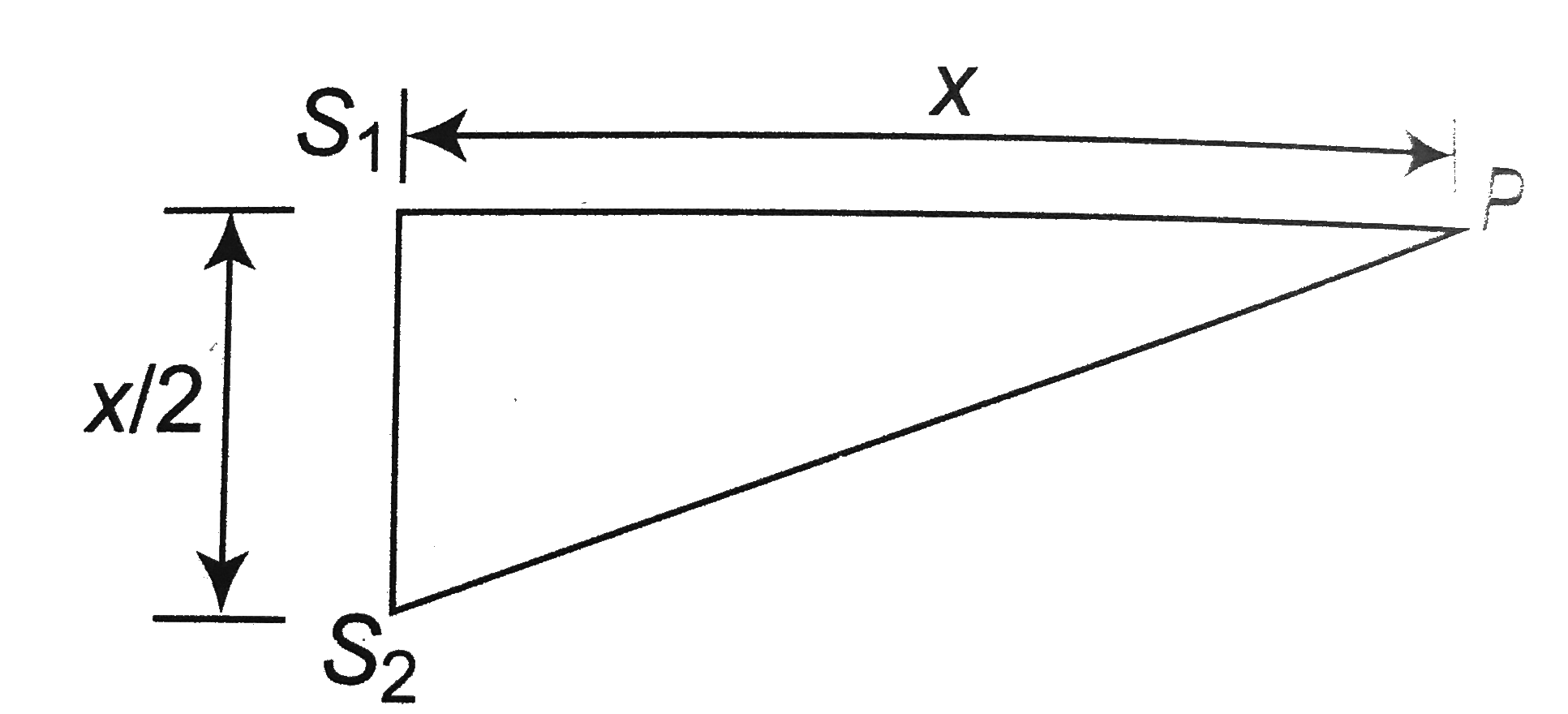
The wavelength of the waves arriving at P from two coherent sources S1 and S2 is 4m, while intensity of each wave is I0. The resultant intensity at P is 2I0. Find the minimum value of S2P
View SolutionIn Youngsdoub≤slitexperiment,thephased⇔erentbetweentwocoherentsourcesofequal∫ensityisπ3.The∫ensityatap∮whichisatequaldistanceomthetwoslitsis(l_@) is maximum intensity)
View Solution
