Two identical thin ring each of radius are co-axially placed at a distance . If the ring have a uniform mass distribution and each has mass and respectively, then the work done in moving a mass from the centre of one ring to that of the other is :
zero
The correct Answer is:B
To find the work done in moving a mass m from the center of one ring to the center of the other ring, we can follow these steps:
Step 1: Understand the Setup
We have two identical thin rings of radius R placed coaxially at a distance R apart. Each ring has a mass m1 and m2 respectively. We need to calculate the gravitational potential at the center of each ring.
Step 2: Calculate the Gravitational Potential at Point A (Center of Ring 1)
The gravitational potential VA at the center of Ring 1 due to Ring 2 can be calculated using the formula:
VA=−Gm2R
where G is the gravitational constant.
Step 3: Calculate the Gravitational Potential at Point B (Center of Ring 2)
Similarly, the gravitational potential VB at the center of Ring 2 due to Ring 1 can be calculated using the distance √2R (the distance from the center of Ring 1 to the center of Ring 2):
VB=−Gm1√2R
Step 4: Calculate the Change in Potential Energy
The work done W in moving the mass m from the center of Ring 1 to the center of Ring 2 is equal to the change in gravitational potential energy:
W=m(VB−VA)
Substituting the values of VA and VB:
W=m(−Gm1√2R−(−Gm2R))
This simplifies to:
W=m(−Gm1√2R+Gm2R)
Step 5: Simplify the Expression
Factoring out G and m:
W=GmR(−m1√2+m2)
Final Result
Thus, the work done in moving the mass m from the center of one ring to the center of the other is:
W=GmR(m2−m1√2)
We have two identical thin rings of radius R placed coaxially at a distance R apart. Each ring has a mass m1 and m2 respectively. We need to calculate the gravitational potential at the center of each ring.
The gravitational potential VA at the center of Ring 1 due to Ring 2 can be calculated using the formula:
VA=−Gm2R
where G is the gravitational constant.
Similarly, the gravitational potential VB at the center of Ring 2 due to Ring 1 can be calculated using the distance √2R (the distance from the center of Ring 1 to the center of Ring 2):
VB=−Gm1√2R
The work done W in moving the mass m from the center of Ring 1 to the center of Ring 2 is equal to the change in gravitational potential energy:
W=m(VB−VA)
Substituting the values of VA and VB:
W=m(−Gm1√2R−(−Gm2R))
This simplifies to:
W=m(−Gm1√2R+Gm2R)
Factoring out G and m:
W=GmR(−m1√2+m2)
Thus, the work done in moving the mass m from the center of one ring to the center of the other is:
W=GmR(m2−m1√2)
Topper's Solved these Questions
Similar Questions
Two identical thin rings each of radius R are coaxially placed at a distance R. If the rings have a uniform mass distribution and each has masses 2m and 4m respectively, then the work done in moving a mass m from centre of one ring to that of the other is
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
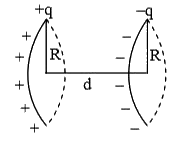
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
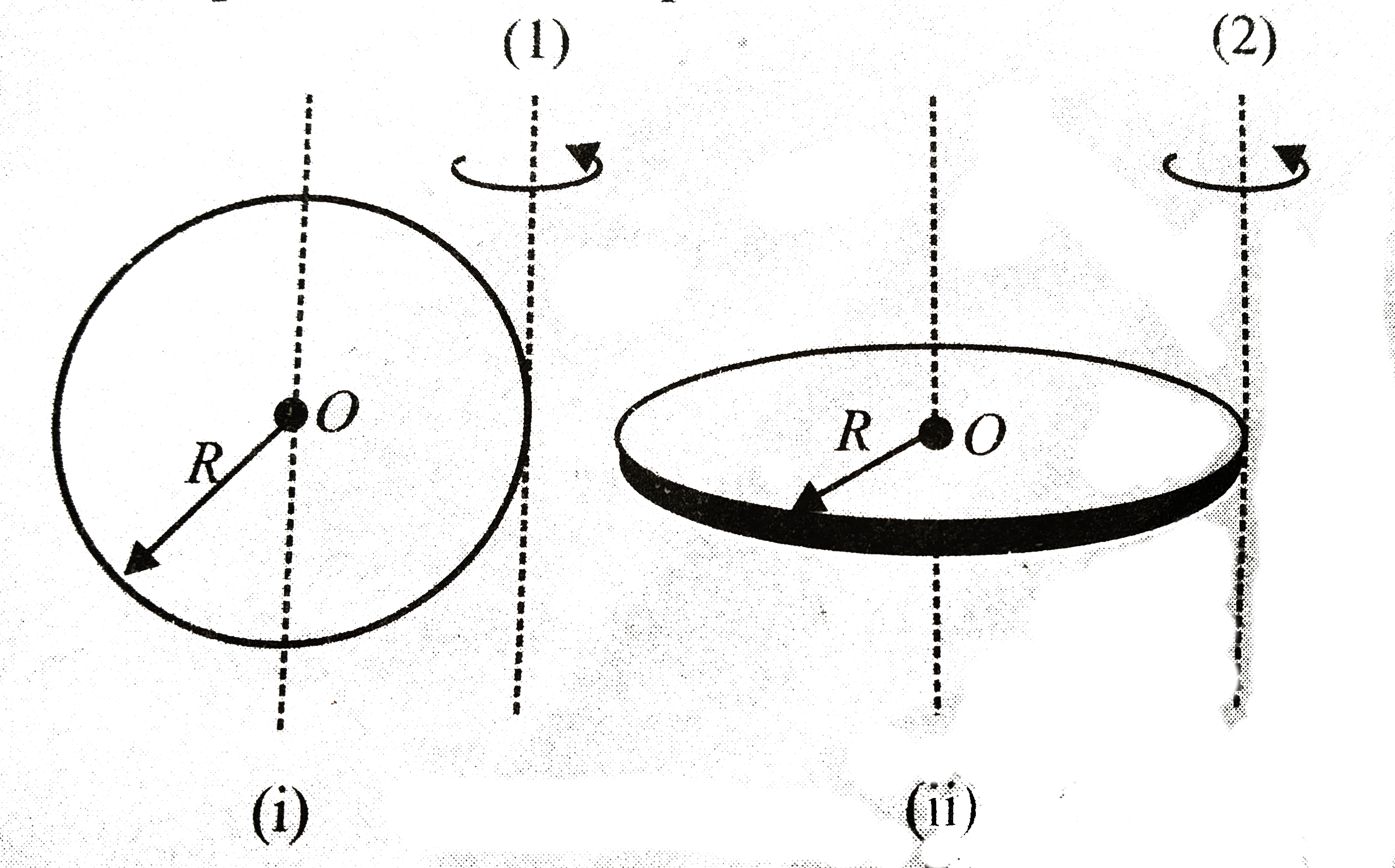
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
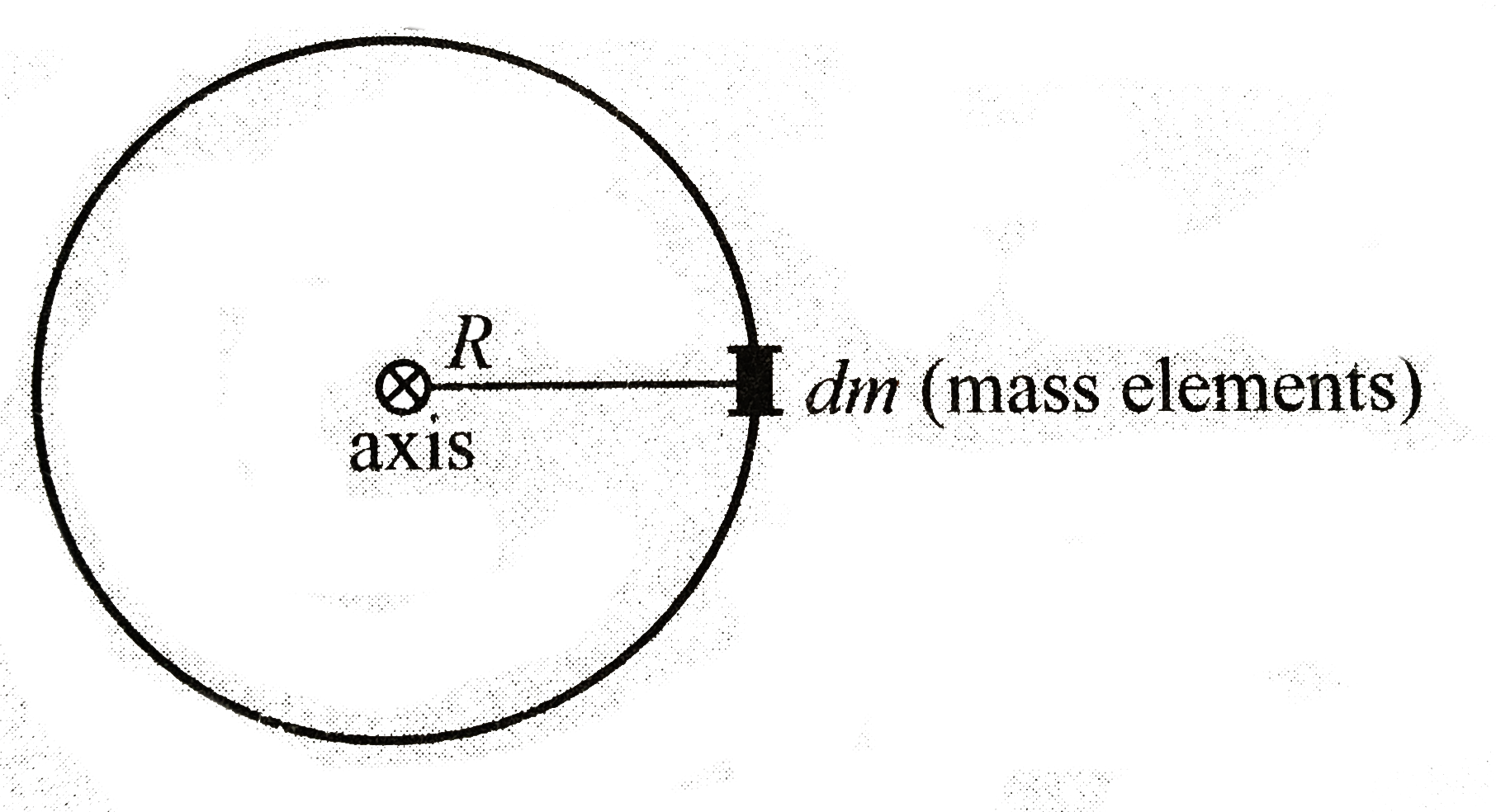
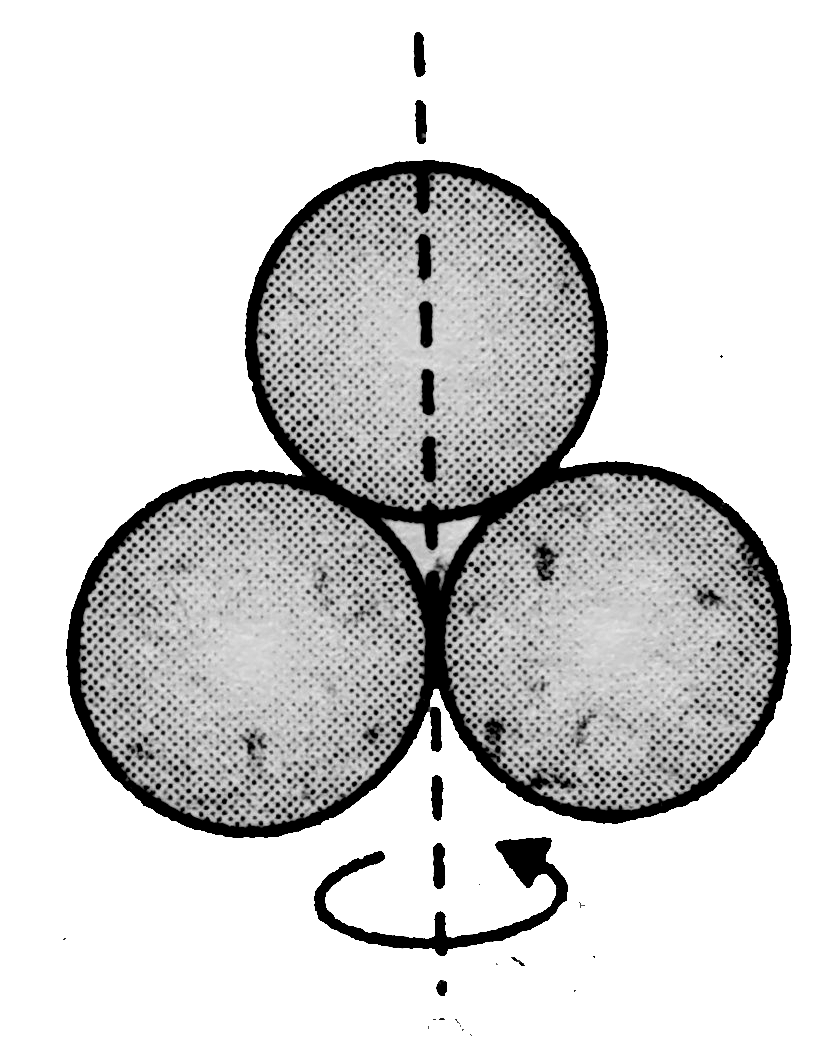
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
View SolutionConsider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
View SolutionA particle of mass 1kg is placed at a distance of 4m from the centre and on the axis of a uniform ring mass 5kg and radius 3m. The work done to increase the distance of the particle from 4m to 3√3m is
View Solution
