Two masses M1 and M2 are connected by light string, which passes over the top of a smooth plane inclined at 30∘ to the horizontal, so that one mass rests on the plane and the other hangs vertically as shown in figure. It is found that M1, hanging vertically can draw M2 up the full length of the plane in half the time in which M2 hanging vertically draws M1 up. Find M1/M2. Assume pulley to be smooth. Initially at time t=0 smooth masses M1=15kg and M2=10kg are held at rest and then they released. if after one second. the string snaps, find the further time taken for the 15 kg mass to return to its original position on the plane. Take g=10m/s2

The correct Answer is:3/2,0.69 sec
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Advance MCQs
17 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
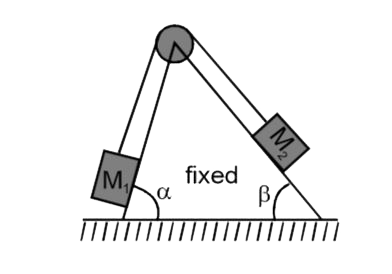
Two masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
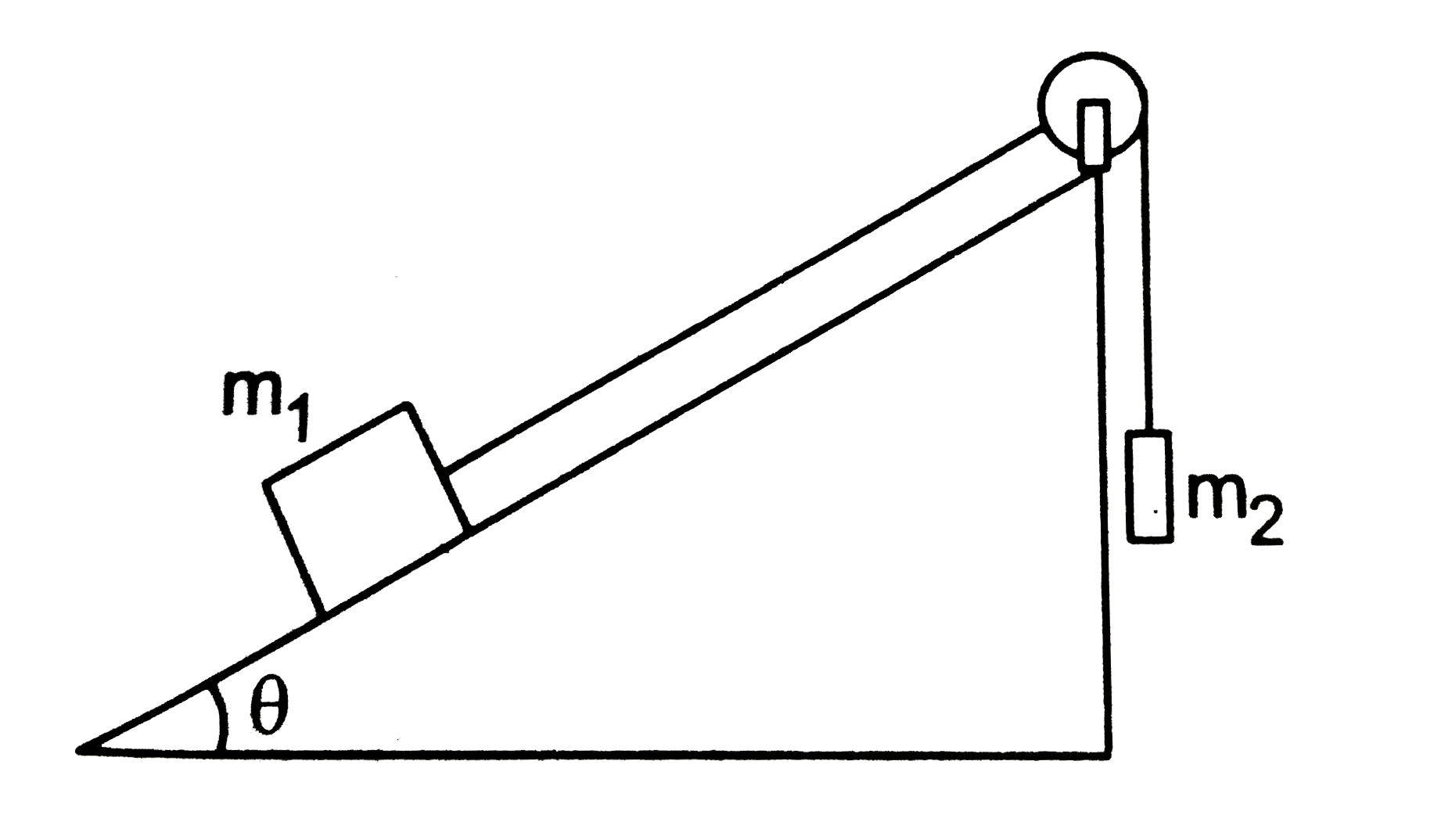
View SolutionTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
View Solution
Knowledge Check
Two masses m1 and m2 are connected by light string, which passes over the top of a smooth plane inclined at 30º to the horizontal, so that one mass rests on the plane and the other hangs vertically as shown in fig. It is found that m1, hanging vertically can draw m2 up the full length of the plane in half the time in which m2 hanging vertically draws m1 up. Find m1/m2 . Assume pulley to be smooth-
 A23B32C47D74
A23B32C47D74Two masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
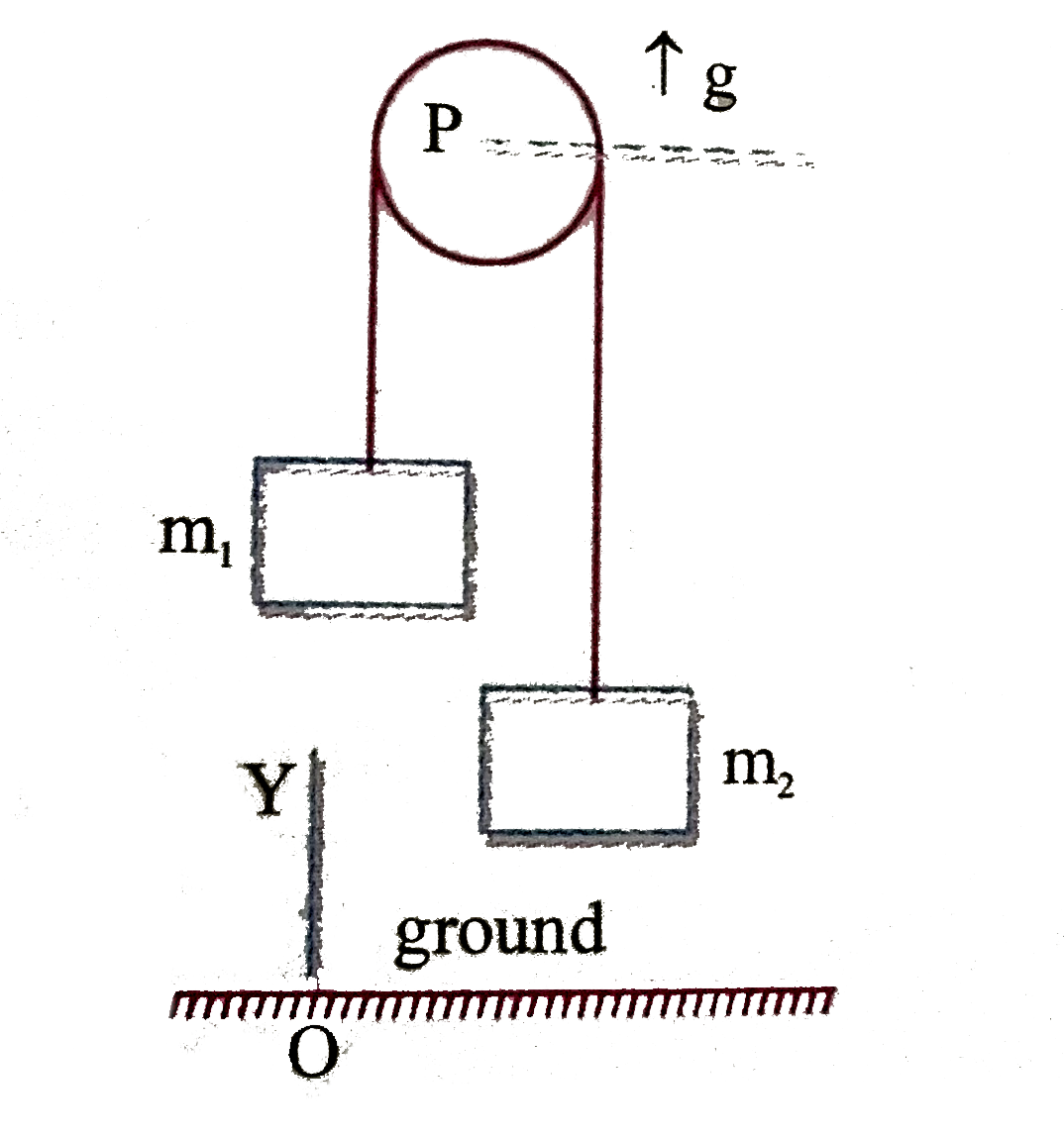 .ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
.ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2gTwo masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:
 Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Two masses M1 and M2 are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30∘ and M1=10kg,M2=5kg. What is the acceleration of mass M2 ?

View SolutionTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.

View SolutionTwo masses M1 and M2 connected by means of a string which is made to pass over light, smooth pulley are in equilibrium on a fixed smooth wedge as shown in figure. If θ=60∘ and α=30∘ then the ratio of M1 to M2 is
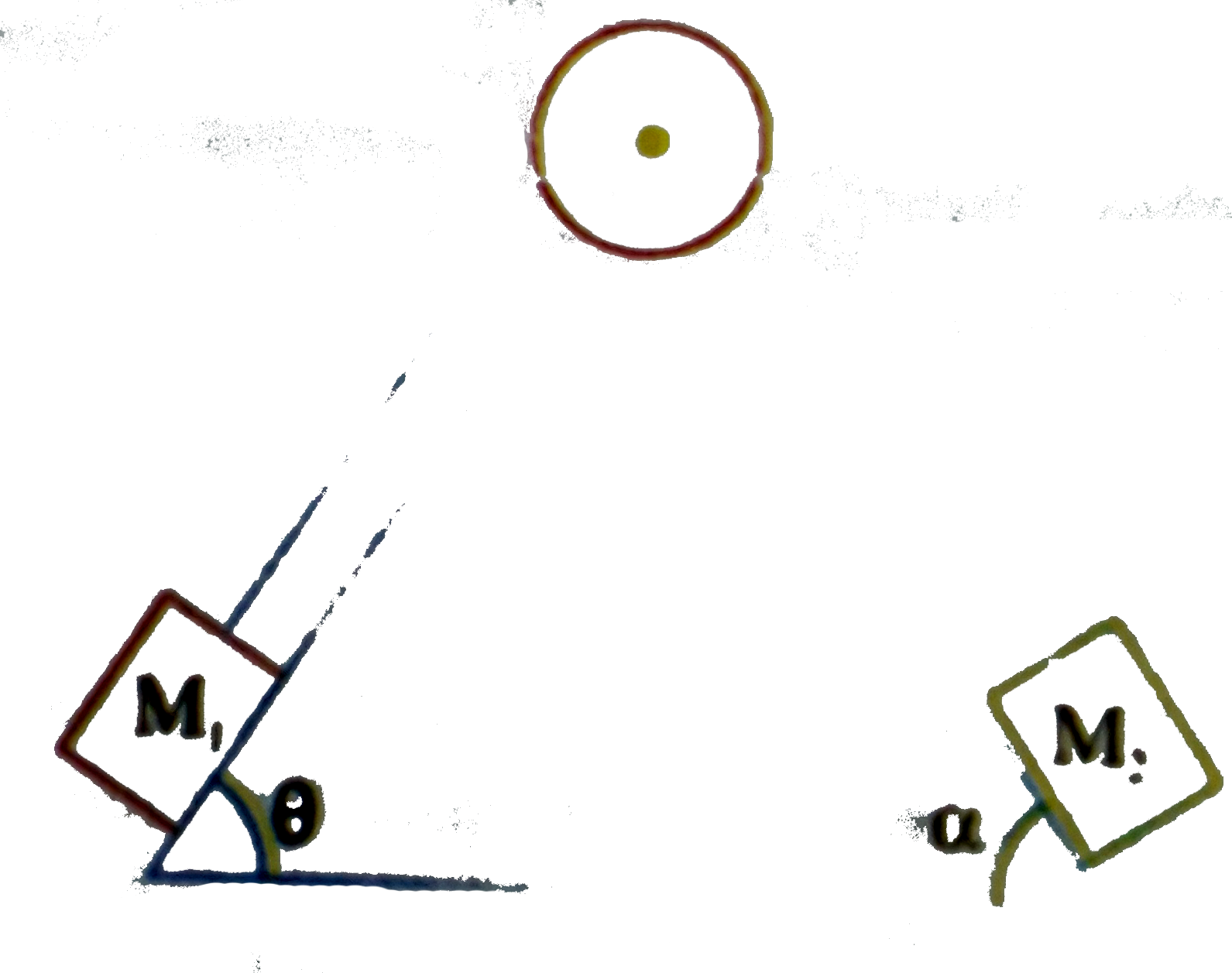 .
.
View SolutionTwo masses M1 and M2 are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30∘ and M1=10kg,M2=5kg. What is the acceleration of mass M2 ?

View SolutionTwo masses M1 and M2 connected by means of a string which is made to pass over light, smooth pulley are in equilibrium on a fixed smooth wedge as shown in figure. If θ=60∘andα=30∘, then the ratio of M1 to M2 is

View Solution
