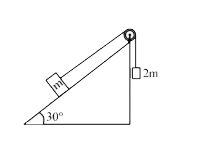
Two bodies of masses are connected by a light string going over a smooth lilght pulley at the end of an incline. The lies on the incline hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
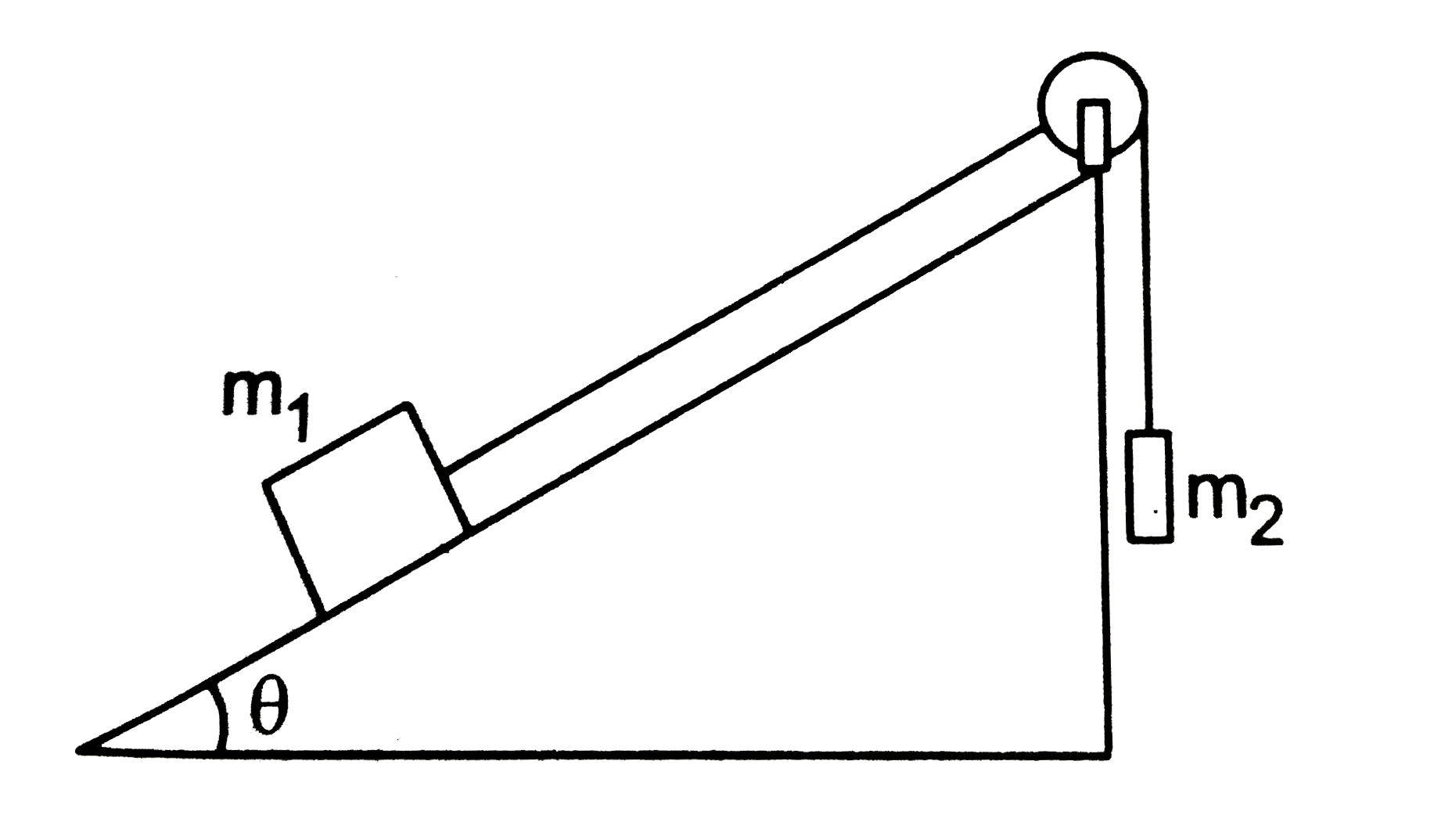
,
,
,
,
The correct Answer is:B
ure shows the situation with the forces onn shown. Take the body of mass as the system. The forces acting on it are
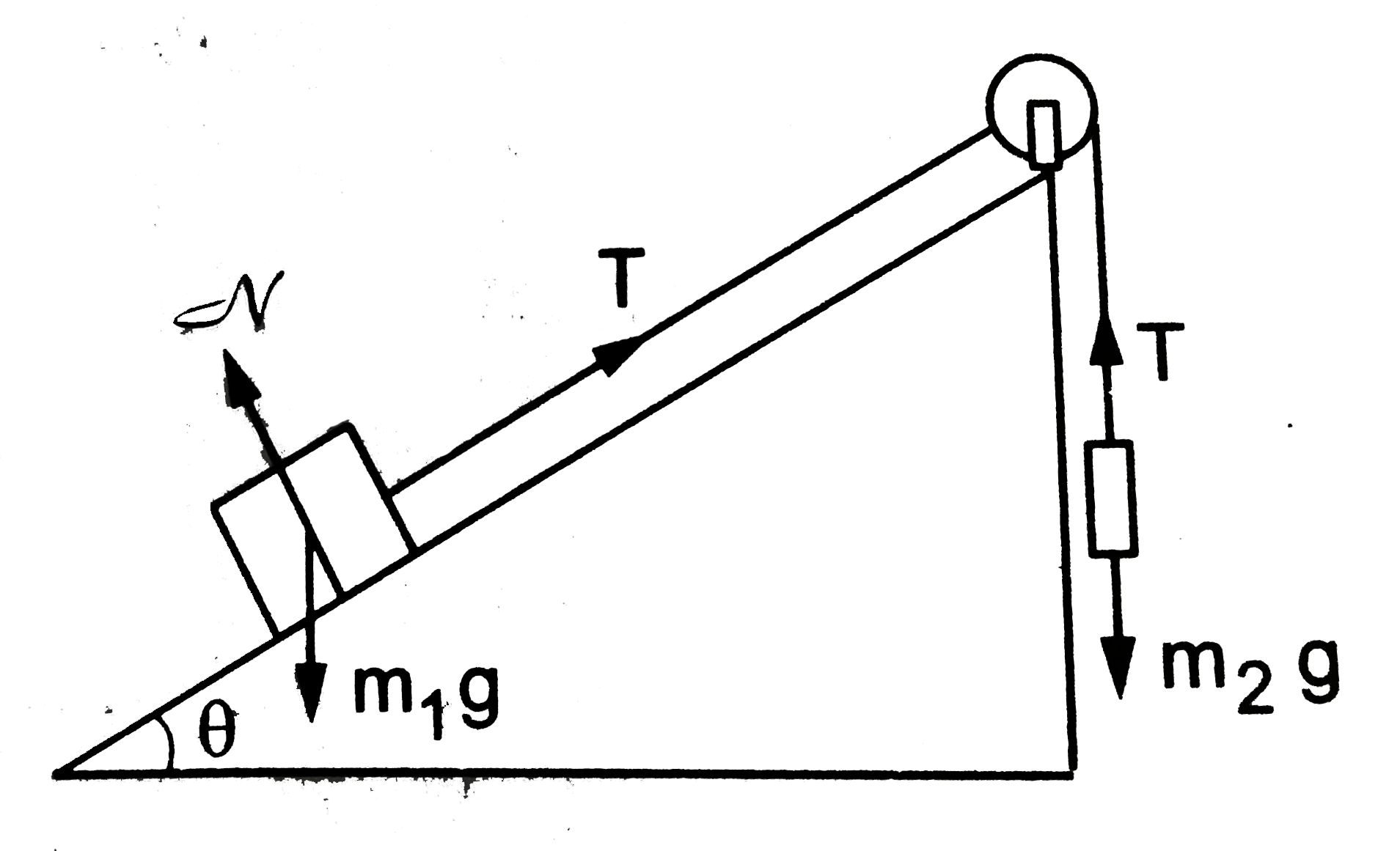
i. g vertically downward (by the earth),
ii. T along the string up the incline (by the string),
N normal to the incline (by the incline).
As the string and the pulley are all light and smooth, the tension in the string is uniform everwhere. Hence, same T is used for the equations of .As the system is in equilibrium, these forces should add to zero.
Take components parallel to the incline,
.........ii
Taking comonents along the normal to the incline,
Taking components along the normal to the incline,
............iii
ElimiN/Ating T form i and ii
or,
theta= sin^-1 (m_2/m_1)N=m_1gsqrt(1- (m_2/m_1)2).
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Short Answer
17 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective 1
14 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
Two blocks of masses 2m and m are connected by a light string going over a pulley of mass 2m and radius R as shown in the figure. The system is released from rest. Find the angular momentum of system when the mass 2m has descended through a height h. Assume no slipping.

View Solutiontwo bodies of masses m and 2m are connected by a light inextensible string passing over a smooth pulley and released After four second a mass m is suddenly joined to the ascending body . Deterinie
(a) the resulting speed ,and
(b) how much kinetic energy is lost by the descending body when the body of mass m is added.
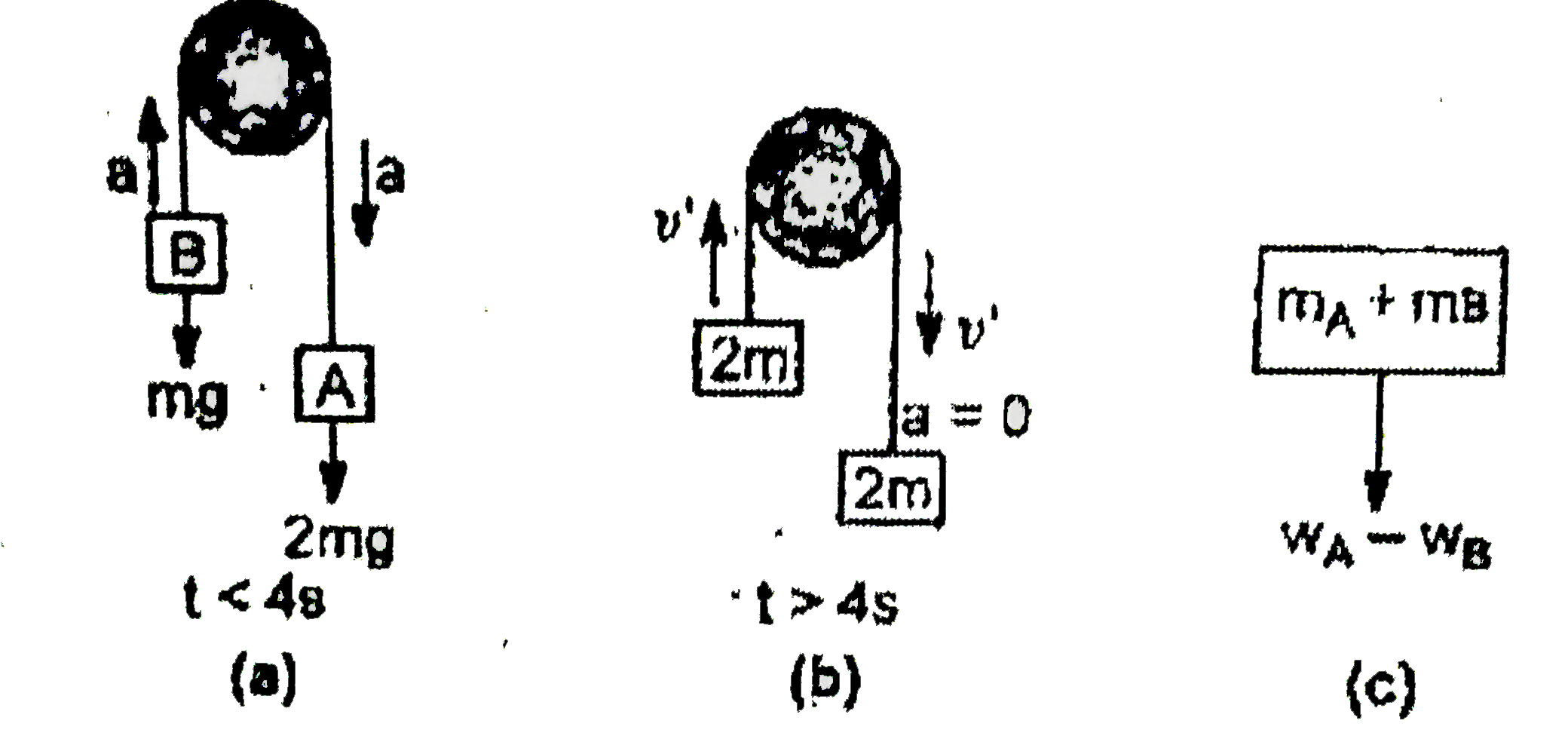
View Solution
Knowledge Check
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)gTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the aboveTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
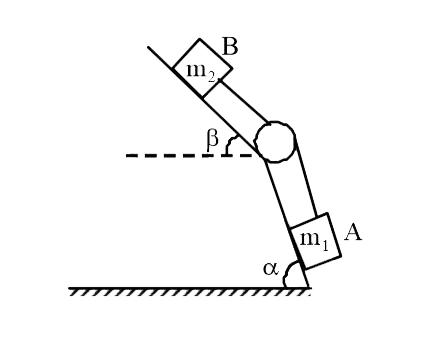
Two blocks A and B of masses m1 and m, are connected by an inextensible string rest on two smooth planes inclined at angle α and β as shown. The tension in string is -
View SolutionTwo blocks of masses m and 2m are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass m is placed on a smooth inclined plane of inclination 30° and 2m hangs vertically. If the system is released, the blocks move with an acceleration equal to :
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of masses is
View Solution
