Two metal rods are fixed end to end between two rigid supports, as shown in figure. Each rod is of length 'l' and area of cross-section is A. When the system is heated up, determine the conditioin whenthe juction between rods does not shift.
[Given, Y1 and Y2 are Young's modulus of materials of the rods, α1 and α2 are coefficient at linear expansion.

(α1Y2
α1Y1=α2Y2
α1=α2
Y1=Y2
b) Since, each rod is prevented from expansion so they are under compression and mechanical strain. The net strain in each rod
ω1lΔT−FIAY1⇒ω2=α2lΔT−FlAY2
ω1=ω2=0
αlΔT−FlAY1=0 and α2lΔT−FlAY2
Solving, we get
α1Y1=α2Y2
Topper's Solved these Questions
- HEAT, TEMPERATURE AND CALORIMETRYBOOK - BITSAT GUIDECHAPTER - HEAT, TEMPERATURE AND CALORIMETRYEXERCISE - Bitsat archives
9 Videos
- GRAVITATIONBOOK - BITSAT GUIDECHAPTER - GRAVITATIONEXERCISE - BITSAT Archives
15 Videos
- LAWS OF THERMODYNAMICSBOOK - BITSAT GUIDECHAPTER - LAWS OF THERMODYNAMICSEXERCISE - 40
1 Videos
Similar Questions
Two metal rods are fixed end to end between two rigid supports as shown in figure. Each rod is of length l and area of cross-section is A. When the systeam is heated up,datermine the condition when the juncation between rods does not shift ? (Y1 and Y2 are Young's modulus of materials of rods, α1 and α2 are coefficients of linear expansion)
_S01_022_Q01.png)
View SolutionTwo same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
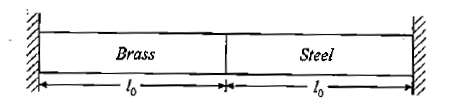
View Solution
Knowledge Check
Two metal rods are fixed end to end between two rigid supports, as shown in figure. Each rod is of length l and area of cross-section is A. When the system is heated up, determine the condition that the junction between rode not shift. [Given Y1andY2 are Young's modulus of materials of teh rods while α1andα2 are coefficient of linear expansion]
 Aα1Y2=α2Y1Bα1Y1=α2Y2Cα1=α2DY1=Y2
Aα1Y2=α2Y1Bα1Y1=α2Y2Cα1=α2DY1=Y2Two rods having length l1 and l2, made of materials with the linear coefficient of expansion α1 and α2 were welded togther. The equivalent coefficients of linear expansion for the obtained rod:-
 Al1α2+l2α1l1+l2Bl1α1+l2α2α1+α2Cl1α1+l2α2l1+l2Dl2α1+l1α2α1+α2
Al1α2+l2α1l1+l2Bl1α1+l2α2α1+α2Cl1α1+l2α2l1+l2Dl2α1+l1α2α1+α2Two rods having length l1andl2 made of materials with the linear expansion coefficient α1andα2 were soldered together. The equivalent coefficients of linear expansion for the obtained rod
Al1α2+l2α1l1+l2Bl1α1+l2α2α1+α2Cl1α1+l2α2l1+l2Dl2α1+l1α2α1+α2
A uniform rod of length (L) and area of cross-section (A) is subjected to tensil load (F). If σ be the Poisson's ratio and Y be the Young's modulus of the material of the rod, then find the volumetric strain produced in the rod.
View SolutionTwo metal rods of the same length and area of cross-section are fixed end to end between rigid supports. The materials of the rods have Young module Y1 and Y2 , and coefficient of linear expansion α1 and α2 . The junction between the rod does not shift and the rods are cooled
View SolutionTwo rods of lengths L1 and L2 are welded together to make a composite rod of length (L1+L2). If the coefficient of linear expansion of the materials of the rod are α1 and α2 respectively. The effective coefficient of linear expansion of the composite rod is
View SolutionA thin rod of negligible mass and area of cross section S is suspended vertically from one end. Length of the rod is L0 at T∘C . A mass m is attached to the lower end of the rod so that when temperature of the rod is reduced to 0∘C its length remains L0 Y is the Young’s modulus of the rod and α is coefficient of linear expansion of rod. Value of m is :
View SolutionTwo rods are joined between fixed supports as shown in the figure. Condition for no change in the length of individual rods with the increase of temperature will be
(α1,α2= linear expansion coefficient
A1,A2= Area of rods
Y1,Y2= Young modulus )
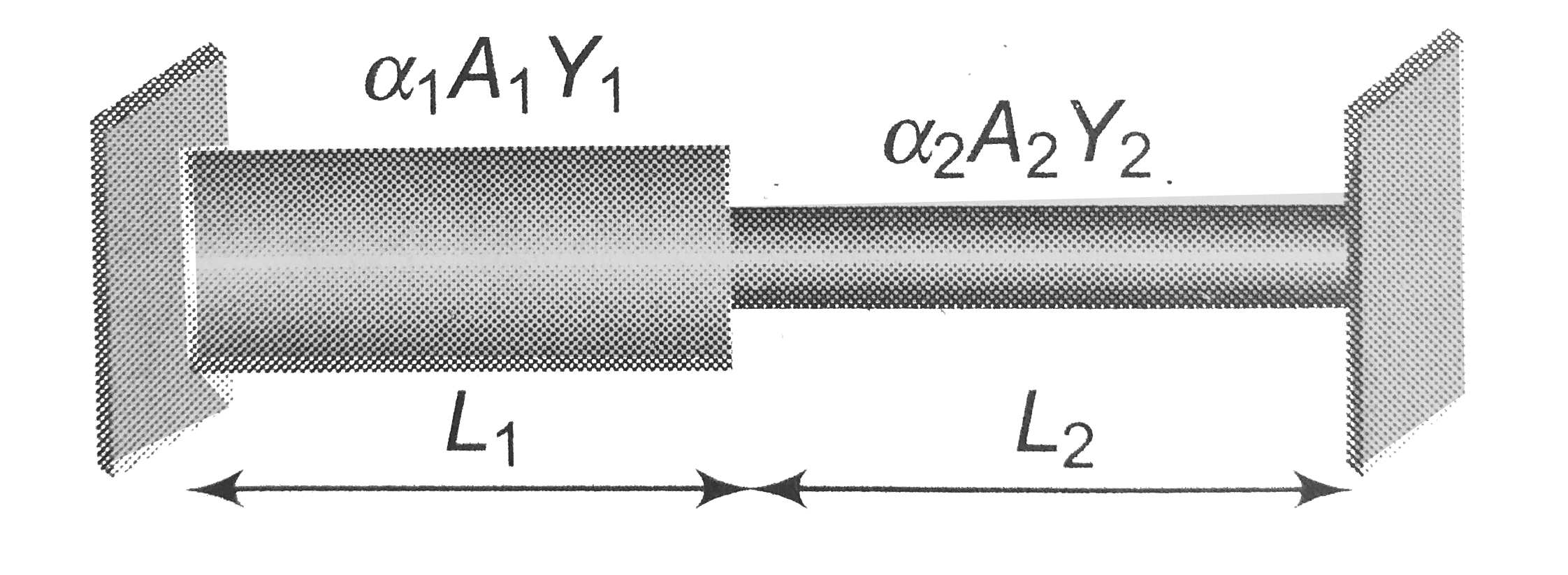
View Solution
