Two painters are working from a wooden hoard 5m long suspended from the top of a building by two ropes attached to the ends of the plank. Either rope can withstand a maximum tension of 1040N. Painter A of mass 80kg is working at a distance of 1m from one end. Painter B of mass 60kg is working at a distance of x in from the centre of mass of the board on the other side. Take mass of the board as 20kg and g=10ms−2. The range of x so that both the painters can work safely is
13<x<116
0<x<116
0<x<2
13<x<2
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the wooden board and ensure that the tensions in the ropes do not exceed the maximum allowable tension of 1040 N. We will use the concept of torque to set up our equations.
1. Identify the Forces Acting on the Board:
- Weight of Painter A (W_A) = mass_A * g = 80 kg * 10 m/s² = 800 N (acting downwards).
- Weight of Painter B (W_B) = mass_B * g = 60 kg * 10 m/s² = 600 N (acting downwards).
- Weight of the board (W_board) = mass_board * g = 20 kg * 10 m/s² = 200 N (acting downwards).
- Tension in the left rope (T_A) and tension in the right rope (T_B) (acting upwards).
2. Set Up the Torque Equation:
- Choose point A (the left end of the board) as the pivot point.
- The total torque about point A must equal zero for the system to be in equilibrium.
3. Calculate the Torque Contributions:
- Torque due to Painter A: τA=WA×dA=800N×1m=800N m (clockwise).
- Torque due to the board: τboard=Wboard×dboard=200N×2.5m=500N m (clockwise).
- Torque due to Painter B: τB=WB×dB=600N×(2.5+x)m (counterclockwise).
- Torque due to Tension B: τTB=TB×5m (counterclockwise).
4. Write the Torque Equation:
τA+τboard=τB+τTB
800+500=600(2.5+x)+TB⋅5
5. Substituting the Maximum Tension:
Since the maximum tension TB can be 1040 N, we substitute this value:
1300=600(2.5+x)+1040⋅5
1300=600(2.5+x)+5200
6. Rearranging the Equation:
600(2.5+x)=1300−5200
600(2.5+x)=−3900
7. Solving for x:
2.5+x=−3900600
2.5+x=−6.5
x=−6.5−2.5
x=−9m (not possible)
8. Adjusting the Tension:
Since the tension cannot exceed 1040 N, we need to find the maximum value of x that keeps the tension below this limit. We can set up the torque equation again with the maximum tension and solve for x.
9. Final Calculation:
After adjusting the calculations for the maximum tension, we find that:
600(2.5+x)=3900
2.5+x=3900600=6.5
x=6.5−2.5=4m
Conclusion:
The range of x so that both painters can work safely is 0≤x≤4m.
- Weight of Painter A (W_A) = mass_A * g = 80 kg * 10 m/s² = 800 N (acting downwards).
- Weight of Painter B (W_B) = mass_B * g = 60 kg * 10 m/s² = 600 N (acting downwards).
- Weight of the board (W_board) = mass_board * g = 20 kg * 10 m/s² = 200 N (acting downwards).
- Tension in the left rope (T_A) and tension in the right rope (T_B) (acting upwards).
- Choose point A (the left end of the board) as the pivot point.
- The total torque about point A must equal zero for the system to be in equilibrium.
- Torque due to Painter A: τA=WA×dA=800N×1m=800N m (clockwise).
- Torque due to the board: τboard=Wboard×dboard=200N×2.5m=500N m (clockwise).
- Torque due to Painter B: τB=WB×dB=600N×(2.5+x)m (counterclockwise).
- Torque due to Tension B: τTB=TB×5m (counterclockwise).
τA+τboard=τB+τTB
800+500=600(2.5+x)+TB⋅5
Since the maximum tension TB can be 1040 N, we substitute this value:
1300=600(2.5+x)+1040⋅5
1300=600(2.5+x)+5200
600(2.5+x)=1300−5200
600(2.5+x)=−3900
2.5+x=−3900600
2.5+x=−6.5
x=−6.5−2.5
x=−9m (not possible)
Since the tension cannot exceed 1040 N, we need to find the maximum value of x that keeps the tension below this limit. We can set up the torque equation again with the maximum tension and solve for x.
After adjusting the calculations for the maximum tension, we find that:
600(2.5+x)=3900
2.5+x=3900600=6.5
x=6.5−2.5=4m
The range of x so that both painters can work safely is 0≤x≤4m.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A fire man has to carry an injured person of mass 40 kg from the top of a building with the help of the rope which can withstand a load of 100 kg. The acceleration of the fireman if his mass is 80 kg, will be-
View SolutionA particle of mass 1kg is placed at a distance of 4m from the centre and on the axis of a uniform ring mass 5kg and radius 3m. The work done to increase the distance of the particle from 4m to 3√3m is
View Solution
Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling . The rod is of mass 'm' and has another weight of mass 2 m hung at a distance of 75 cm from A . The tension in the string at A is :
View SolutionA monkey of mass 20 kg climbs on a rope which can stand a maximum tension of 300 N. In which of the following case will the rope break . The monkey
View SolutionA wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA uniform wooden plank of mass 150 kg and length 8 m is floating on still water with a man of 50 kg at one end of it . The man walks to the other end of the plank and stops. Than the distance covered by the plank is
View SolutionA uniform rope of length 5m is on a smooth horizontal surface. It is being pulled by a horizontal force of 20 N at one end. The ratio of tension at a distance of 2m from force end to tension at a distance of 2m from free end is,
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
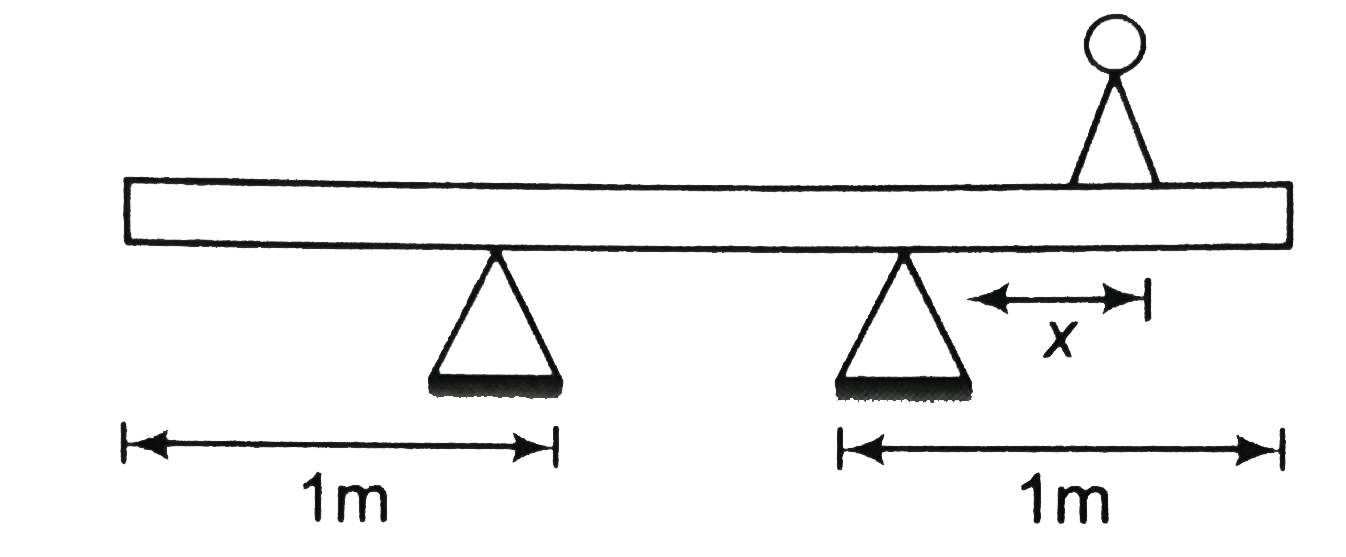
View SolutionA horizontal plank is 10.0m long with uniform density and mass 10kg .It rests on two supports which are placed 1.0m from each end as shown in the figure. A man of mass 80 kg can stand upto distance x on the plank without causing it to tip .The value of x is
View SolutionA 24 kg block resting on a floor has a rope tied to its top. The maximum tension , the rope can withstand without breaking is 310 N . The minimum time in which the block can be lifted a vertical distance of 4.6 m by pulling on the rope is
View Solution
