A 24 kg block resting on a floor has a rope tied to its top. The maximum tension , the rope can withstand without breaking is 310 N . The minimum time in which the block can be lifted a vertical distance of 4.6 m by pulling on the rope is
1.2s
1.3s
1.7s
2.3s
The correct Answer is:C
To solve the problem step by step, we will follow these steps:
Step 1: Identify the forces acting on the block
The block has two main forces acting on it:
- The gravitational force (weight) acting downwards, which is given by W=mg.
- The tension in the rope acting upwards, which is given as T.
Step 2: Calculate the weight of the block
Given:
- Mass of the block m=24kg
- Acceleration due to gravity g≈10m/s2
The weight of the block can be calculated as:
W=mg=24kg×10m/s2=240N
Step 3: Set up the equation of motion
According to Newton's second law, the net force acting on the block is equal to the mass of the block multiplied by its acceleration a:
T−W=ma
Substituting the values we have:
T−240=24a
Step 4: Substitute the maximum tension into the equation
The maximum tension T that the rope can withstand is given as 310N. Substituting this into the equation:
310−240=24a
70=24a
Step 5: Solve for acceleration a
Now, we can solve for a:
a=7024=3512m/s2≈2.92m/s2
Step 6: Use the kinematic equation to find the time
We need to find the minimum time t to lift the block a vertical distance s=4.6m. Using the kinematic equation:
s=ut+12at2
Since the initial velocity u=0:
s=12at2
Rearranging for t:
t2=2sa
t=√2sa
Step 7: Substitute the values to find t
Substituting s=4.6m and a=3512m/s2:
t=
⎷2×4.63512
t=√9.2×1235=√110.435≈√3.15≈1.77s
Final Answer
The minimum time in which the block can be lifted a vertical distance of 4.6 m is approximately 1.77 seconds.
---
The block has two main forces acting on it:
- The gravitational force (weight) acting downwards, which is given by W=mg.
- The tension in the rope acting upwards, which is given as T.
Given:
- Mass of the block m=24kg
- Acceleration due to gravity g≈10m/s2
W=mg=24kg×10m/s2=240N
According to Newton's second law, the net force acting on the block is equal to the mass of the block multiplied by its acceleration a:
T−W=ma
Substituting the values we have:
T−240=24a
The maximum tension T that the rope can withstand is given as 310N. Substituting this into the equation:
310−240=24a
70=24a
Now, we can solve for a:
a=7024=3512m/s2≈2.92m/s2
We need to find the minimum time t to lift the block a vertical distance s=4.6m. Using the kinematic equation:
s=ut+12at2
Since the initial velocity u=0:
s=12at2
Rearranging for t:
t2=2sa
t=√2sa
Substituting s=4.6m and a=3512m/s2:
t=
⎷2×4.63512
t=√9.2×1235=√110.435≈√3.15≈1.77s
The minimum time in which the block can be lifted a vertical distance of 4.6 m is approximately 1.77 seconds.
Similar Questions
The maximum tension a rope can withstand is 60 kg.wt. The ratio of maximum acceleration with which two boys of masses 20 kg and 30 kg can climb up the rope at the same time is
View SolutionA 10 kg stone is suspended with a rope of breaking strength 30 kg-wt. The minimum time in which the stone can be raised through a height 10 m starting from rest is (Take, g=10Nkg−1).
View SolutionA stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal circle. The maximum tension the string can withstand is 16 Newton . The maximum velocity of revolution that can be given to the stone without breaking it, will be
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View SolutionA body of mass 50 kg and specific gravity force is to be lifted using a rope of breaking strength of 60 kg wt. The acceleration with which it can be pulled up in least interval of time
View SolutionTwo painters are working from a wooden hoard 5m long suspended from the top of a building by two ropes attached to the ends of the plank. Either rope can withstand a maximum tension of 1040N. Painter A of mass 80kg is working at a distance of 1m from one end. Painter B of mass 60kg is working at a distance of x in from the centre of mass of the board on the other side. Take mass of the board as 20kg and g=10ms−2. The range of x so that both the painters can work safely is
View SolutionA balloon is tied to a block. The mass of the block is 2kg. The tension of the string between the balloon and the block is 30N. Due to the wind, the string has an angle 0 relative to the vertical direction. cosθ=4/5and sinθ=3/5. Assume the acceleration due to gravity is g=10m/s2. Also assume the block is small so the force on the block from the wind can be ignored. Then the x-component and the y-component of the acceleration a of the block.
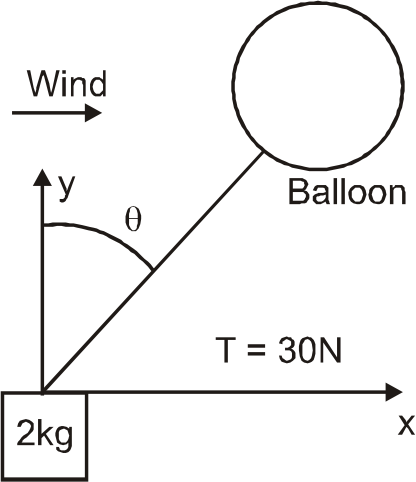
View SolutionA balloon is tied to a block. The mass of the block is 2kg. The tension of the string between the balloon and the block is 30N. Due to the wind, the string has an angle 0 relative to the vertical direction. cosθ=4/5and sinθ=3/5. Assume the acceleration due to gravity is g=10m/s2. Also assume the block is small so the force on the block from the wind can be ignored. Then the x-component and the y-component of the acceleration a of the block.

View SolutionA monkey of mass 20 kg climbs on a rope which can stand a maximum tension of 300 N. In which of the following case will the rope break . The monkey
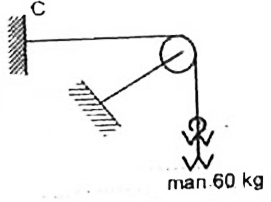
View SolutionOne end of a massless rope, which passes over a massless and frictionless pulley P is tied to fixed hook C, while the other end is free. Maximum tension that the rope can bear is 960 N. With what value of max. safe acceleration (m/s2) can a man of 60 kg climb on the rope?
View Solution
