Two particle of mass m and 2m, connected by a massless rod, slide on t

Two beads of mass $2 m$ and $m$ , connected by a rod of length $l$ and of negligible mass are free to move in a smooth vertical circular wire frame of radius $l$ as shown. Initially the system is held in horizontal position $($ Refer figure $)$

The velocity that should be given to mass $2 m ($ when rod is in horizontal position $)$ in counter $-$ clockwise direction so that the rod just becomes vertical is $:$
A $\sqrt{\frac{5 g l}{3}}$
B $\sqrt{(\frac{3 \sqrt{3} - 1}{3}) g l}$
C $\sqrt{\frac{3}{2} g l}$
D $\sqrt{\frac{5}{2} g l}$
Two particles A and B connected by a rigid rod AB. The rod slides along two perpendicular rails as shown. The velocity of A to the left is 10 m/s. What is the velocity of B, when angle $θ$ is $37^{\circ}$ ?

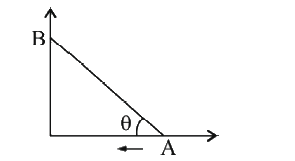A $5.8 m / s$
B $9.8 m / s$
C $11.2 m / s$
D $13.3 m / s$
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
A $T = M g$
B $T > M g$
C $T < M g$
D $T = M g + M g$

Two particles A and B connected by a rigid rod AB. The rod slides along two perpendicular rails as shown. The velocity of A to the left is 10 m/s. What is the velocity of B, when angle $θ$ is $37^{\circ}$ ?