Two particles 1 and 2 start simultaneously from origin and move along the positive X direction. Initial velocity of both particles is zero. The acceleration of the two particles depends on their displacement (x) as shown in fig.
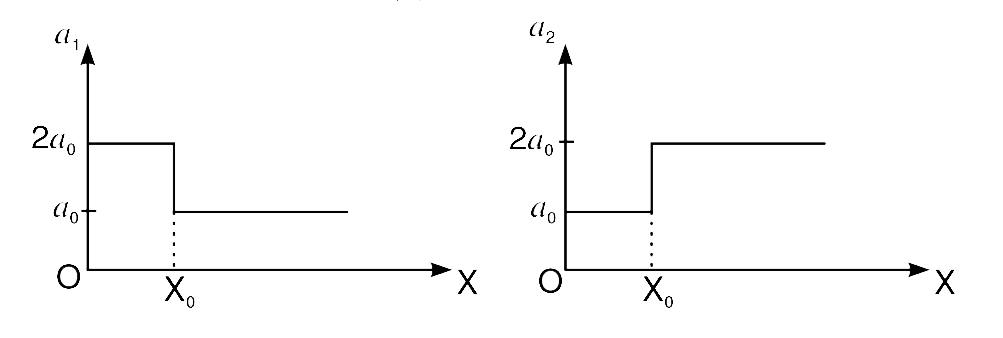
(a) Particles 1 and 2 take t1 and t2 time respectively for their displacement to become x0. Find t2t1.
(b) Which particle will cover 2x0 distance in least time? Which particle will cross the point x=2x0 with greater speed?
(c) The two particles have same speed at a certain time after the start. Calculate this common speed in terms of a0 and x0.
The correct Answer is:(a) √2 (b) particle 1 will cover 2x0 in lesser time. Both will cross 2x0 with same speed. (c) v=(2+√2)√a0x0
Topper's Solved these Questions
Similar Questions
Two friends A and B are running on a circular track of perimeter equal to 40 m. At time t=0 they are at same location running in the same direction. A is running slowly at a uniform speed of 4.5km/hr whereas B is running swiftly at a speed of 18km/hr.
(a) At what time t0 the two friends will meet again?
(b) What is average velocity of A and B for the interval t=0 to t=t0?
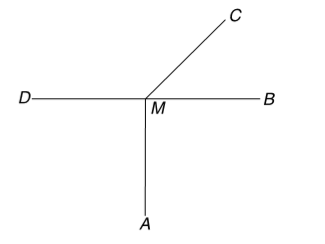
View SolutionFour metal rods each of length L and cross sectional area A are joined at point M. Thermal conductivities of MA, MB and MD are equal and that of MC is thrice that of MA. The end points A, B, C and D are kept in large reservoirs. Heat folws into the junction from B at a rate of P(Js−1) and C from at a rate of 3P. Heat flows out of D at a rate of 5P.
(a) Find the relation between temperatures of points A, B and C.
(b) Find temperature of D if temperature of A and M and TA and TM respectively.
View SolutionAn ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy

View SolutionConsider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time t_(1) , the particle is at point P, where its co-ordinate is x_(1) and at time t_(2) , the particle is at point Q, where its co-ordinate is x_(2) . The displacement during the time interval from t_(1) to t_(2) is the vector from P to Q, the x-component of this vector is (x_(2) - x_(1)) and all other components are zero. It is convenient to represent the quantity x_(2) - x_(1) the change in x by means of a notation Delta , thus Delta x = x_(2) - x_(1) and Delta t = t_(2) - t_(1) . The average velocity bar(V) = (x_(2) - x_(1))/(t_(2) - t_(1)) = (Delta x)/(Delta t) A particle moves half the time of its journey with u . The rest of the half time it moves with two velocities v_(1) and v_(2) such that half the distance it covers with v_(1) and the other half with v_(2) . The net average velocity is: (Assume straight line motion)
View SolutionA particle is moving along a straight line. Its displacement-time graph is shown {:(,,"Column-I",,"Column-II"),(,(A),"Work done on particle from 0 to "t_(1),(P),"Positive"),(,(B),"Work done on particle from " t_(1) " to " t_(2),(Q),"Negative"),(,(C),"Work done on particle from " t_(2) " to " t_(3),(R),"zero"),(,(D),"Work done on particle from " t_(3) " to " t_(4),(S),"Unpredectible"):}
View SolutionA particle starts moving at t = 0 in a circle of radius R = 2m with constant angular acceleration of a - 3 "rad/sec"^(2) . Initial angular speed of the particle is 1 rad/sec. At time t_(0) the angle between the acceleration vector and the velocity vector of the particle is 37^(@) . What is the magnitude of the acceleration of the particle at t_(0) ?
View Solutionएक सरल रेखा में गति करते कण की t1=1 सेकण्ड पर स्थिति x1=12 मीटर है तथा t2=3 सेकण्ड पर स्थिति x2=4 मीटर है । इस समय - अंतराल में विस्थापन तथा औसत वेग ज्ञात कीजिए ।
View Solutionएक कण x=Asinωt के अनुसार सरल आवर्त गति कर रहा है | यदि कण को x = 0 से x=√3A/2 तक पहुँचने में समय t1 तथा x=√3A/2 से x=A तक पहुँचने में समय t2 लगता है तो t1/t2 का मान होगा :
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View SolutionA particle crosses points A, B, C in a straight line at a constant acceleration. The particle travels from A to B in time t1 and B to C in time t2 . If AB = a , BC = b then prove that the acceleration of the particle is 2(bt1−at2)/t1t2(t1+t2).
View SolutionIf the time taken by a particle moving at constant acceleration to travel equal distances along a straight line are t_(1), t_(2), t_(3) respectively prove that (1)/(t_(1))-(1)/(t_(2))+(1)/(t_(3))=(3)/(t_(1)+t_(2)+t_(3)) .
View SolutionThe displacement of a particle undergoing S.H.M. as a function of time t is given by
x=Asin(4πt3)
Where x is in cm and t in second
The time taken by the particle to travel from (a) x = 0 to A/2 is ta and time taken by it to travel from (b) x = A/2 to A is tb. Calculate the ratio tb/ta.
View SolutionFollowing are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S). a) V_(av)=(1)/(2)[v(t_(1))+v(t_(2))] b) V_(av)=(r(t_(2))-r(t_(2)))/(t_(2)-t_(1)) c)r= (1)/(2)(v(t_(2))-v(t_(1))(t_(2)-t_(1)) d) a_(av)=(v(t_(2))-v(t_(1)))/(t_(2)-t_(1))
View SolutionA particle executes SHM of type x=Asinωt. It takes time t1 from x=0 to x=A2andt2 from x=A2 to x=A. The ratio t1:t2 will be
View SolutionAt two particular closest instants of time t1 and t2, the displacements of a particle performing SHM are equal. At these instants.
View Solution
