Two particles A and B , each carrying charge Q are held fixed with a separation D between them. A particle C having mass m and charge q is kept at the middle point of the line AB. If particle C is displaced through a distance x along the line AB. What will be the time period of the oscillations.
To find the time period of oscillations of particle C, we can follow these steps:
Step 1: Understand the Configuration
We have two fixed charges, A and B, each with charge Q, separated by a distance D. The charge C with mass m and charge q is initially placed at the midpoint between A and B, which is at a distance of D2 from both A and B.
Step 2: Displacement of Charge C
When charge C is displaced by a distance x along the line AB, the new distances from A and B become:
- Distance from A: D2+x
- Distance from B: D2−x
Step 3: Calculate the Forces Acting on Charge C
The force on charge C due to charge A is given by Coulomb's law:
FA=14πϵ0Qq(D2+x)2
The force on charge C due to charge B is:
FB=14πϵ0Qq(D2−x)2
Step 4: Determine the Net Force
The net force F acting on charge C will be the difference between the two forces, taking into account their directions:
F=FA−FB=14πϵ0⎛⎜
⎜⎝Qq(D2+x)2−Qq(D2−x)2⎞⎟
⎟⎠
Step 5: Simplify the Expression
Using the approximation for small displacements x (i.e., x≪D2), we can use the binomial expansion to simplify:
(D2+x)−2≈(D2)−2(1−4xD)
(D2−x)−2≈(D2)−2(1+4xD)
Substituting these approximations into the force equation gives:
F≈14πϵ0⋅Qq⋅(4xD3)
Step 6: Relate Force to Acceleration
Using Newton's second law, F=ma:
ma=4Qq4πϵ0D3x
Thus, the acceleration a can be expressed as:
a=4Qq4πϵ0mD3x
Step 7: Formulate the Equation of Motion
This is a simple harmonic motion equation of the form a=−ω2x, where:
ω2=4Qq4πϵ0mD3
Step 8: Calculate the Time Period
The time period T of oscillation is given by:
T=2π√mk=2π
⎷m4Qq4πϵ0D3
This simplifies to:
T=2π√4πϵ0mD34Qq
Final Answer
Thus, the time period of the oscillations of particle C is:
T=2π√πϵ0mD3Qq
We have two fixed charges, A and B, each with charge Q, separated by a distance D. The charge C with mass m and charge q is initially placed at the midpoint between A and B, which is at a distance of D2 from both A and B.
When charge C is displaced by a distance x along the line AB, the new distances from A and B become:
- Distance from A: D2+x
- Distance from B: D2−x
The force on charge C due to charge A is given by Coulomb's law:
FA=14πϵ0Qq(D2+x)2
The force on charge C due to charge B is:
FB=14πϵ0Qq(D2−x)2
The net force F acting on charge C will be the difference between the two forces, taking into account their directions:
F=FA−FB=14πϵ0⎛⎜
⎜⎝Qq(D2+x)2−Qq(D2−x)2⎞⎟
⎟⎠
Using the approximation for small displacements x (i.e., x≪D2), we can use the binomial expansion to simplify:
(D2+x)−2≈(D2)−2(1−4xD)
(D2−x)−2≈(D2)−2(1+4xD)
Substituting these approximations into the force equation gives:
F≈14πϵ0⋅Qq⋅(4xD3)
Using Newton's second law, F=ma:
ma=4Qq4πϵ0D3x
Thus, the acceleration a can be expressed as:
a=4Qq4πϵ0mD3x
This is a simple harmonic motion equation of the form a=−ω2x, where:
ω2=4Qq4πϵ0mD3
The time period T of oscillation is given by:
T=2π√mk=2π
⎷m4Qq4πϵ0D3
This simplifies to:
T=2π√4πϵ0mD34Qq
Thus, the time period of the oscillations of particle C is:
T=2π√πϵ0mD3Qq
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Two particles A and B , each carrying charge Q are held fixed with a separation D between them. A particle C having mass m and charge q is kept at the middle point of the line AB. (a) If it is displaced throught a distance x perpendicular to AB, what would be the electric force experienced by it .(b) Assuming x ltltd, show that this force is proportional to x. (c) under what conditions will the paricle C execute simple harmonic motion if it is released after such a small displacement? Find the time period of the oscillations if these conditions are satisfied.
View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
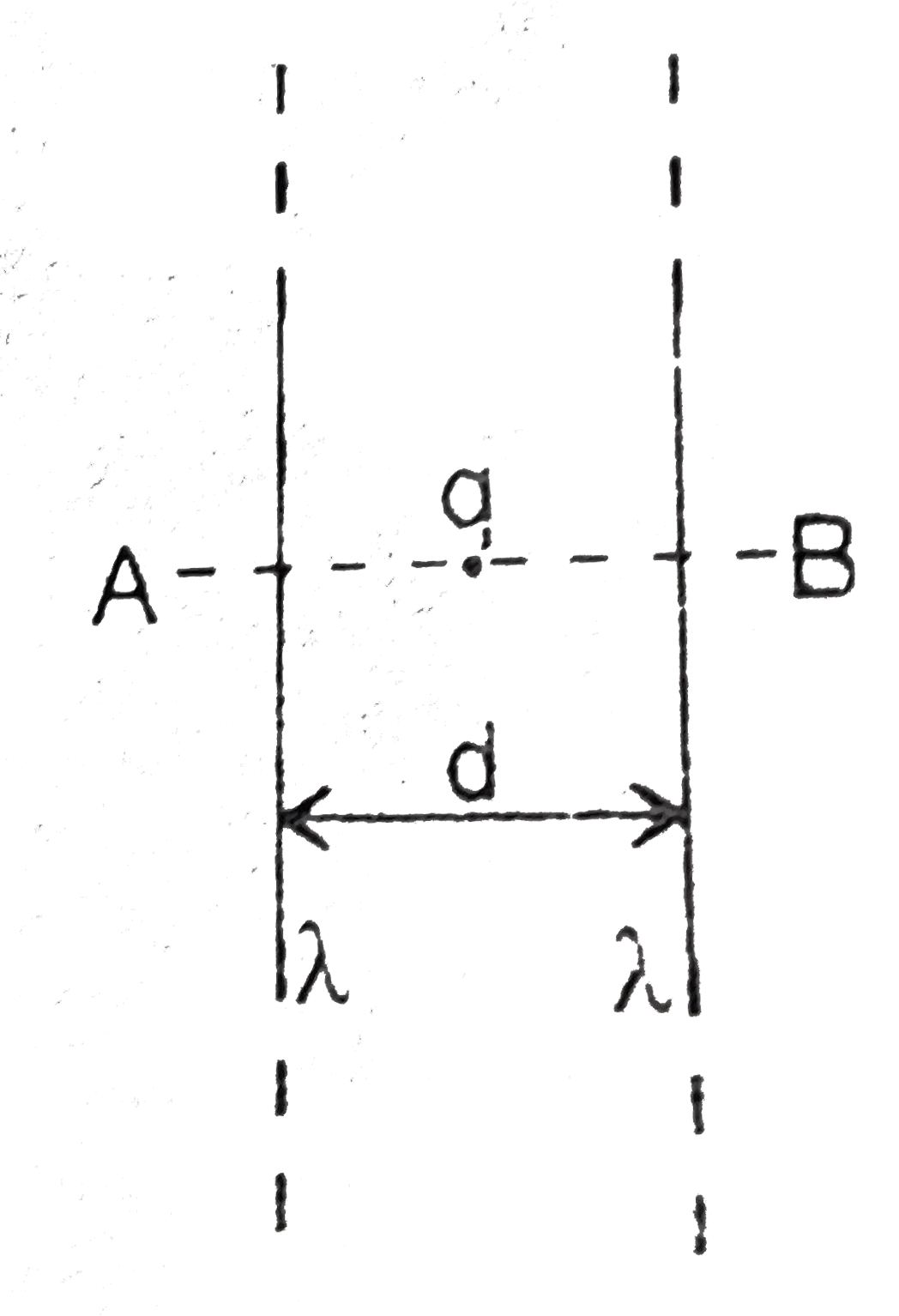
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionTwo particles A and B having charges q and 2q respectively are placed on a smooth table with a separation d. A third particle C is to be clamped on the table in such a way that the particles A and B remain at rest on the table under electrical forces. What should be the charge on C and where should it clamped?
View SolutionA negatively charged particle is situated on a straight line joining two other stationary particles each having charge +q. The direction of the motion of the negatively charged particle will depend on
View SolutionTwo charges, each equal to q, aer kept at x=−a and x=a on the x-axis. A particle of mass m and charge q0=q2 is placed at the origin. If charge q0 is given a small displacement (ylt lt a) along the y-axis, the net force acting on the particle is proportional to
View SolutionTwo small particles P and Q each of mass m are fixed along x-axis at points (a,0) and (-a,0). A third particle R is kept at origin. Then
View SolutionTwo particles, each of mass m, are a distance d apart. To bring a third particle, also having mass m, from far away to the point midway between the two particles an external agent does work given by:
View Solution
