Two particles A and B, move with constant velocities →v1 and →v2. At the initial moment their position vectors are →r1 and →r2 respectively. The condition for particle A and B for their collision is
→r1−→r2=→v1−→v2
→r1−→r2∣∣→r1−→r2∣∣=→v2−→v1∣∣→v2−→v1∣∣
→r1.→v1=→r2.→v2
→r1×→v1=→r2×→v2
The correct Answer is:B
To determine the condition for the collision of two particles A and B moving with constant velocities, we need to analyze their motion using the equations of motion in vector form.
1. Define the Position Vectors:
Let the position vectors of particles A and B at time t be given by:
→rA(t)=→r1+→v1t
→rB(t)=→r2+→v2t
2. Set the Condition for Collision:
For the two particles to collide, their position vectors must be equal at the same time t:
→rA(t)=→rB(t)
3. Equate the Position Vectors:
Substituting the expressions for →rA(t) and →rB(t):
→r1+→v1t=→r2+→v2t
4. Rearranging the Equation:
Rearranging gives:
→r1−→r2=(→v2−→v1)t
5. Solving for Time t:
If we denote →rAB=→r1−→r2 and →vAB=→v2−→v1, we can express the time t when the collision occurs as:
t=→rAB→vAB
This equation implies that for the particles to collide, the vector →rAB must be parallel to →vAB.
6. Condition for Collision:
Therefore, the condition for the collision of particles A and B is that the vector →rAB must be parallel to the vector →vAB:
→rAB×→vAB=0
Final Condition:
The final condition for the collision of the two particles A and B is:
(→r1−→r2)×(→v2−→v1)=0
Let the position vectors of particles A and B at time t be given by:
→rA(t)=→r1+→v1t
→rB(t)=→r2+→v2t
For the two particles to collide, their position vectors must be equal at the same time t:
→rA(t)=→rB(t)
Substituting the expressions for →rA(t) and →rB(t):
→r1+→v1t=→r2+→v2t
Rearranging gives:
→r1−→r2=(→v2−→v1)t
If we denote →rAB=→r1−→r2 and →vAB=→v2−→v1, we can express the time t when the collision occurs as:
t=→rAB→vAB
This equation implies that for the particles to collide, the vector →rAB must be parallel to →vAB.
Therefore, the condition for the collision of particles A and B is that the vector →rAB must be parallel to the vector →vAB:
→rAB×→vAB=0
The final condition for the collision of the two particles A and B is:
(→r1−→r2)×(→v2−→v1)=0
Topper's Solved these Questions
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.5 Inertial and non-inertial frames)
2 Videos
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.6 Moment of force)
3 Videos
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.3 Law of conservation of momentum)
21 Videos
- ELECTRONS AND PHOTONSBOOK - TARGET PUBLICATIONCHAPTER - ELECTRONS AND PHOTONSEXERCISE - Evaluation Test
19 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
Similar Questions
Two particles, 1 and 2, move with constant velocities v1 and v2. At the initial moment their radius vectors are equal to r1 and r2. How must these four vectors be interrelated for the particles to collide?
View SolutionThe position vector of A , B are →aand→b respectively. The position vector of C is (5→a3)−→bthen
View Solution
Knowledge Check
Two point masses 1 and 2 move with uniform velocities →v1 and →v2, respectively. Their initial position vectors are →r1 and →r2, respectively. Which of the following should be satisfied for the collision of the point masses?
A→r1−→r2|→r2−→r1|=→v2−→v1|→v2−→v1|B→r2−→r1|→r2−→r1|=→v2−→v1|→v2−→v1|C→r2−→r1|→r2+→r1|=→v2−→v1|→v2+→v1|D→r2−→r1|→r2+→r1|=→v2−→v1|→v2+→v1|If two bodies are in motion with velocity →v1 and →v2:
A|vrel|=√v21+v22B|→–––(rel)|=v1±v2∣Cvre=0Dvrel>c (speed of light)Two particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
AzeroB(m1+m2)gt0C2(m1+m2)gt0D12(m1+m2)gt0
Two particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .
.
View SolutionParticle A of mass m1 moving with velocity (√3ˆi+ˆj)ms−1 collides with another particle Bof mass m2 which is at rest initially. Let →V1and→V2 be the velocities of particles A and B after collision respectively. If m1=2m2 and after collision →V1−(ˆi+√3ˆj)ms−1, the angle between →V1and→V2 is :
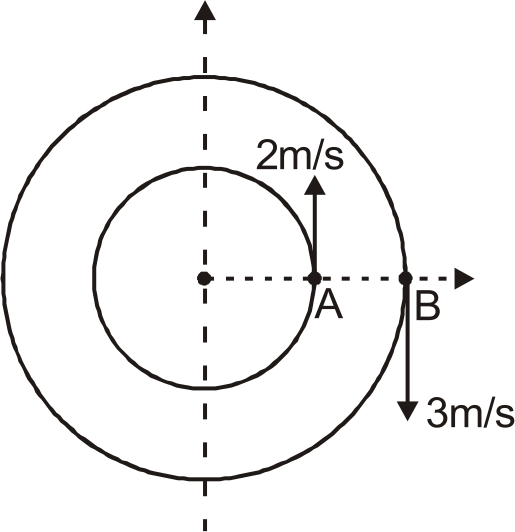
View SolutionTwo particles A and B are revolving with constant angular velocity on two concentric circles of radius 1m and 2m respectively as shown in figure. The positions of the particles at t = 0 are shown in figure. The positions of the particles at t=0 are shown in figure. if mA=2kg,mB=1kg and →PA and →PB are linear momentum of the particle then what is the maximum value of ∣∣→PA+→PB∣∣ in kg-m/sec in subsequent motion of two particles.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionIf →F is the force acting in a particle having position vector →r and →τ be the torque of this force about the origin, then
View Solution
