Two particles A and B move with constant velocity →v1 and →v2 along two mutually perpendicular straight lines towards intersection point O as shown in figure, At moment t = 0 particles were located at distance l1 and l2 respectively from O. Then minimu distance between the particles and time taken are respectively
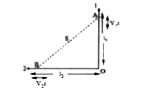
|l1v2−l2v1|√v21+v22,l1v1+l2v2v21+v22
|l1v1−l2v2|√v21+v22,l1v2+l2v1v21+v22
|l1v2−l2v1|√v21+v22,√l1l2,(l1v1+l2v2)l1(v21+v22)l2
|l1v2−l2v1|√v21+v22,√l1l2,(l1v1+l2v2)l2(v21+v22)l1
The correct Answer is:A
Step by step video & image solution for Two particles A and B move with constant velocity vec(v_1) and vec(v_2) along two mutually perpendicular straight lines towards intersection point O as shown in figure, At moment t = 0 particles were located at distance l_1 and l_2 respectively from O. Then minimu distance between the particles and time taken are respectively by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A STRAIGHT LINE
59 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
Two particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionTwo ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them will be shortest at t= ........
View SolutionTwo ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them will be shortest at t= ........
View SolutionTwo particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .
.
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View SolutionTwo particles, 1 and 2, move with constant velocities v1 and v2. At the initial moment their radius vectors are equal to r1 and r2. How must these four vectors be interrelated for the particles to collide?
View SolutionTwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is

View SolutionA particle of mass m moves in the XY plane with constant velocity v along the straight line PQ as shown in the figure. Its angular momentum with respect to origin O is(θ is angle between→v and x-axis)

View SolutionTwo particles are moving along two long straight lines, in the same plane with same speed equal to 20cm/s. The angle between the two linse is 60∘ and their intersection point isO. At a certain moment, the two particles are located at distances 3m and 4m from O and are moving twowards O. Subsequently, the shortest distance between them will be
View SolutionTwo particles A and B are moving as shown in figure. At this moment of time, the angular speed of A with respect to B is?
View Solution
