Two ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them will be shortest at t= ........
2bˆj
aˆj
(a−2b)ˆi
None of these
The correct Answer is:A
To solve the problem of finding the time at which the distance between the two ships V and W is shortest, we can follow these steps:
Step 1: Define the positions of the ships
At time t=0:
- Ship V is located at a distance of 100m from point O and moves towards O with a velocity of 2m/s.
- Ship W is located at a distance of 200m from point O and moves towards O with a velocity of 4m/s.
Step 2: Write the position equations for the ships
After time t:
- The position of Ship V from point O will be:
xV=100−2t
- The position of Ship W from point O will be:
yW=200−4t
Step 3: Write the distance formula between the two ships
Since the ships are moving along two perpendicular tracks, the distance L between them at time t can be expressed using the Pythagorean theorem:
L=√(100−2t)2+(200−4t)2
Step 4: Simplify the distance formula
Expanding the expression under the square root:
L=√(100−2t)2+(200−4t)2
=√(10000−400t+4t2)+(40000−1600t+16t2)
=√20000−2000t+20t2
Step 5: Minimize the distance
To find the time t at which the distance L is minimized, we need to minimize L2 (since the square root function is monotonically increasing):
L2=20000−2000t+20t2
Step 6: Differentiate and set to zero
Now, we differentiate L2 with respect to t:
d(L2)dt=−2000+40t
Setting the derivative equal to zero for minimization:
−2000+40t=0
40t=2000
t=200040=50seconds
Conclusion
The distance between the ships V and W will be shortest at t=50 seconds.
---
At time t=0:
- Ship V is located at a distance of 100m from point O and moves towards O with a velocity of 2m/s.
- Ship W is located at a distance of 200m from point O and moves towards O with a velocity of 4m/s.
After time t:
- The position of Ship V from point O will be:
xV=100−2t
- The position of Ship W from point O will be:
yW=200−4t
Since the ships are moving along two perpendicular tracks, the distance L between them at time t can be expressed using the Pythagorean theorem:
L=√(100−2t)2+(200−4t)2
Expanding the expression under the square root:
L=√(100−2t)2+(200−4t)2
=√(10000−400t+4t2)+(40000−1600t+16t2)
=√20000−2000t+20t2
To find the time t at which the distance L is minimized, we need to minimize L2 (since the square root function is monotonically increasing):
L2=20000−2000t+20t2
Now, we differentiate L2 with respect to t:
d(L2)dt=−2000+40t
Setting the derivative equal to zero for minimization:
−2000+40t=0
40t=2000
t=200040=50seconds
The distance between the ships V and W will be shortest at t=50 seconds.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 35videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 46videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 15videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
Two particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionTwo particles A and B move with constant velocity →v1 and →v2 along two mutually perpendicular straight lines towards intersection point O as shown in figure, At moment t = 0 particles were located at distance l1 and l2 respectively from O. Then minimu distance between the particles and time taken are respectively
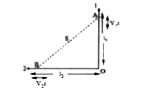 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two points A and B located in diametrically opposite directions of a point charge of +2μC at distances 2.0 m and 1.0 m respectively from it. Determine the potential difference VA−VB
A3×103VB6×104VC−9×103VD−3×103V
Two particles are moving along two long straight lines, in the same plane with same speed equal to 20cm/s. The angle between the two linse is 60∘ and their intersection point isO. At a certain moment, the two particles are located at distances 3m and 4m from O and are moving twowards O. Subsequently, the shortest distance between them will be
View SolutionA body moves along a straight line OAB simple harmonically. It has zero velocity at the points A and B which are at distances 'a' and b'respectivelyom0' and has velocity 'V' when halfway between them then the period of SHM
View SolutionTwo trains are moving with velocities v1=10ms−1andv2=20ms−1 on the same track in opposite directions. After the application of brakes if their retarding rates are a1=2ms−2anda2=1ms−2 respectively, then the minimum distance of separation between the trains to avoid collision is
View SolutionTwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is
 View Solution
View SolutionThe length of tangents from two given points to a given circle are t1andt2. If the two points are conjugate to each other w.r.t. the given circle, prove that the distance between the points will be √t21+t22.
View SolutionA point mass 10 g moves in the xy plane with a velocity 2ms−1 along a straight line. Find the magnitude and direction of its angular momentum (i) with respect to the origin O and (ii) with respect to the origin O. The magnitude of the position vector →r is 0.5 m and the angle θ=30∘.
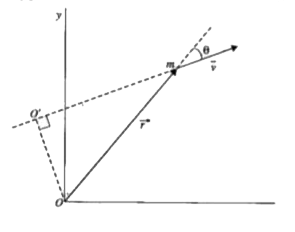 View Solution
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
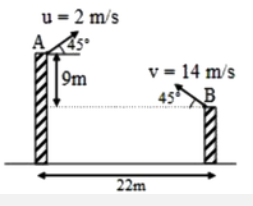 View Solution
View Solution

