Two particles are in SHM along same line. Time period of each is T and amplitude is A. After how much time will they collide if at time t=0. (a) first particle is at x1=+A2 and moving towards positive x - axis and second particle is at x2=−A√2 and moving towards negative x - axis, (b) rest information are same as mentioned in part (a) except that particle first is also moving towards negative x - axis.
The correct Answer is:A, B, D
To solve the problem, we need to analyze the motion of both particles in simple harmonic motion (SHM) and determine when they collide based on their initial positions and directions of motion.
Part (a):
1. Initial Positions and Directions:
- Particle 1 is at x1=+A2 and moving towards the positive x-axis.
- Particle 2 is at x2=−A√2 and moving towards the negative x-axis.
2. Angular Displacement Calculation:
- For Particle 1, the angular displacement θ1 can be calculated using:
cos(θ1)=x1A=A2A=12⟹θ1=60∘=π3 radians
- For Particle 2, the angular displacement θ2 is:
cos(θ2)=x2A=−A√2A=−1√2⟹θ2=135∘=3π4 radians
3. Relative Motion:
- Both particles will collide when the sum of the distances they cover equals the total distance between them.
- The total angular distance from θ1 to θ2 is:
θ=θ2−θ1=3π4−π3
- Finding a common denominator (12):
θ=9π12−4π12=5π12
4. Calculating Time to Collision:
- The angular velocity ω for both particles is given by:
ω=2πT
- The time t taken for them to collide is given by:
ωt=5π12⟹2πTt=5π12
- Solving for t:
t=5T24
Part (b):
1. Initial Positions and Directions:
- The initial positions remain the same, but now Particle 1 is also moving towards the negative x-axis.
2. Angular Displacement:
- The angular displacements remain the same as calculated before:
- Particle 1: θ1=π3
- Particle 2: θ2=3π4
3. Relative Motion:
- Since both particles are now moving towards negative x, we need to consider their combined angular motion:
- The total angular distance they need to cover to collide is still θ=θ2−θ1=5π12.
4. Calculating Time to Collision:
- The equation for time remains:
ωt=5π12
- However, since both are moving towards each other, they will cover the distance faster. The effective angular distance covered is doubled:
2ωt=5π12
- Solving for t:
t=5T48
Final Answers:
- (a) The time after which the particles collide is t=5T24.
- (b) The time after which the particles collide is t=5T48.
1. Initial Positions and Directions:
- Particle 1 is at x1=+A2 and moving towards the positive x-axis.
- Particle 2 is at x2=−A√2 and moving towards the negative x-axis.
- For Particle 1, the angular displacement θ1 can be calculated using:
cos(θ1)=x1A=A2A=12⟹θ1=60∘=π3 radians
- For Particle 2, the angular displacement θ2 is:
cos(θ2)=x2A=−A√2A=−1√2⟹θ2=135∘=3π4 radians
- Both particles will collide when the sum of the distances they cover equals the total distance between them.
- The total angular distance from θ1 to θ2 is:
θ=θ2−θ1=3π4−π3
- Finding a common denominator (12):
θ=9π12−4π12=5π12
- The angular velocity ω for both particles is given by:
ω=2πT
- The time t taken for them to collide is given by:
ωt=5π12⟹2πTt=5π12
- Solving for t:
t=5T24
1. Initial Positions and Directions:
- The initial positions remain the same, but now Particle 1 is also moving towards the negative x-axis.
- The angular displacements remain the same as calculated before:
- Particle 1: θ1=π3
- Particle 2: θ2=3π4
- Since both particles are now moving towards negative x, we need to consider their combined angular motion:
- The total angular distance they need to cover to collide is still θ=θ2−θ1=5π12.
- The equation for time remains:
ωt=5π12
- However, since both are moving towards each other, they will cover the distance faster. The effective angular distance covered is doubled:
2ωt=5π12
- Solving for t:
t=5T48
- (a) The time after which the particles collide is t=5T24.
- (b) The time after which the particles collide is t=5T48.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.1
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Two particles are in SHM along same line with same amplitude A and same time period T. At time t=0, particle 1 is at + A2 and moving towards positive x-axis. At the same time particle 2 is at −A2 and moving towards negative x-axis. Find the timewhen they will collide.
View SolutionA particle is moving with speed v=b√x along positive x-axis. Calculate the speed of the particle at time t=τ (assume tha the particle is at origin at t= 0).
View SolutionTwo particles are executing SHM in a straight line. Amplitude A and the time period T of both the particles are equal. At time t=0, one particle is at displacement x1=+A and the other x2=(−A2) and they are approaching towards each other. After what time they across each other? T4
View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
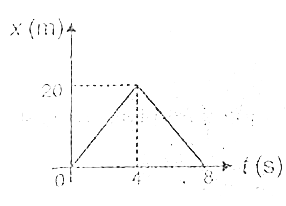
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionA particle moves along the X-axis as x=u(t−2s)+a(t−2s)2.
View SolutionTwo particles undergo SHM along the same line with the same time period (T) and equal amplitude (A). At a particular instant one is at x=−A and the other is at x=0. If they start moving in the same direction then they will cross each other at

(i) t=4T3 (ii) t=3T8 (iii) x=A2 (iv) x=A√2
View SolutionTwo particles are in SHM with same amplitude A and same regualr frequency ω. At time t=0, one is at x =+A2 and the other is at x=−A2. Both are moving in the same direction.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View SolutionA particle moves along x-axis according to relation x=1+2sinωt. The amplitude of S.H.M. is
View Solution
