Two particles are moving along x-axis. Particle-1 is 40m behind Particle-2. Particle-1 starts with velocity12m/s and acceleration 4m/s2 both in positive x-direction. Particle-2 starts with velocity 4m/s and acceleration 12m/s2 also in positive x-direction. Find
(a) the time when distance between them is minimum.
(b) the minimum distacne between them.
The correct Answer is:A, B, C
To solve the problem, we will follow these steps:
Step 1: Set Up the Equations for Each Particle
We need to find the equations of motion for both particles.
- For Particle 1:
- Initial position s1(0)=−40m (since it is 40 m behind Particle 2)
- Initial velocity u1=12m/s
- Acceleration a1=4m/s2
The position of Particle 1 at time t is given by:
s1(t)=s1(0)+u1t+12a1t2
Substituting the values:
s1(t)=−40+12t+12⋅4⋅t2=−40+12t+2t2
- For Particle 2:
- Initial position s2(0)=0 (starting at the origin)
- Initial velocity u2=4m/s
- Acceleration a2=12m/s2
The position of Particle 2 at time t is given by:
s2(t)=s2(0)+u2t+12a2t2
Substituting the values:
s2(t)=0+4t+12⋅12⋅t2=4t+6t2
Step 2: Find the Time When the Velocities are Equal
To find the time when the distance between the two particles is minimum, we need to set their velocities equal to each other.
The velocity of Particle 1 at time t is:
v1=u1+a1t=12+4t
The velocity of Particle 2 at time t is:
v2=u2+a2t=4+12t
Setting v1=v2:
12+4t=4+12t
Rearranging gives:
12−4=12t−4t⟹8=8t⟹t=1s
Step 3: Calculate the Distances Travelled by Each Particle at t=1s
Now, we will calculate the distance travelled by each particle at t=1s.
- Distance travelled by Particle 1:
s1(1)=−40+12(1)+2(12)=−40+12+2=−26m
- Distance travelled by Particle 2:
s2(1)=4(1)+6(12)=4+6=10m
Step 4: Find the Minimum Distance Between the Particles
The minimum distance between the two particles at t=1s is given by:
Minimum Distance=s2(1)−s1(1)=10−(−26)=10+26=36m
Final Answers
(a) The time when the distance between them is minimum is t=1s.
(b) The minimum distance between them is 36m.
We need to find the equations of motion for both particles.
- Initial position s1(0)=−40m (since it is 40 m behind Particle 2)
- Initial velocity u1=12m/s
- Acceleration a1=4m/s2
s1(t)=s1(0)+u1t+12a1t2
Substituting the values:
s1(t)=−40+12t+12⋅4⋅t2=−40+12t+2t2
- Initial position s2(0)=0 (starting at the origin)
- Initial velocity u2=4m/s
- Acceleration a2=12m/s2
s2(t)=s2(0)+u2t+12a2t2
Substituting the values:
s2(t)=0+4t+12⋅12⋅t2=4t+6t2
To find the time when the distance between the two particles is minimum, we need to set their velocities equal to each other.
v1=u1+a1t=12+4t
The velocity of Particle 2 at time t is:
v2=u2+a2t=4+12t
12+4t=4+12t
Rearranging gives:
12−4=12t−4t⟹8=8t⟹t=1s
Now, we will calculate the distance travelled by each particle at t=1s.
s1(1)=−40+12(1)+2(12)=−40+12+2=−26m
s2(1)=4(1)+6(12)=4+6=10m
The minimum distance between the two particles at t=1s is given by:
Minimum Distance=s2(1)−s1(1)=10−(−26)=10+26=36m
(a) The time when the distance between them is minimum is t=1s.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 3
1 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 4
1 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 1
1 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Two particles are moving along x-axis. Particle-1 starts from x=−10m with velocity 4m/s along negative x-direction and acceleration 2m/s2 along positive x-direction. Particle-2 starts from x=+2m with velocity 6m/s along positive x-direction and acceleration 2m/s2 along negative x-direction.
(a) Find the time when they collide.
(b) Find the x-coordinates where they collide. Both start simultaneously.
View SolutionA particle starts with a velocity of 2m/s and moves in a straight line with a retardation of 0.1m/s2. The time that it takes to describe 15m is
View SolutionParticle A is moving along X-axis. At time t = 0, it has velocity of 10ms−1 and acceleration −4ms−2. Particle B has velocity of 20ms−1 and acceleration −2ms−2. Initially both the particles are at origion. At time t = 2 distance between the particles are at origin. At time t = 2 s distance between the particles is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
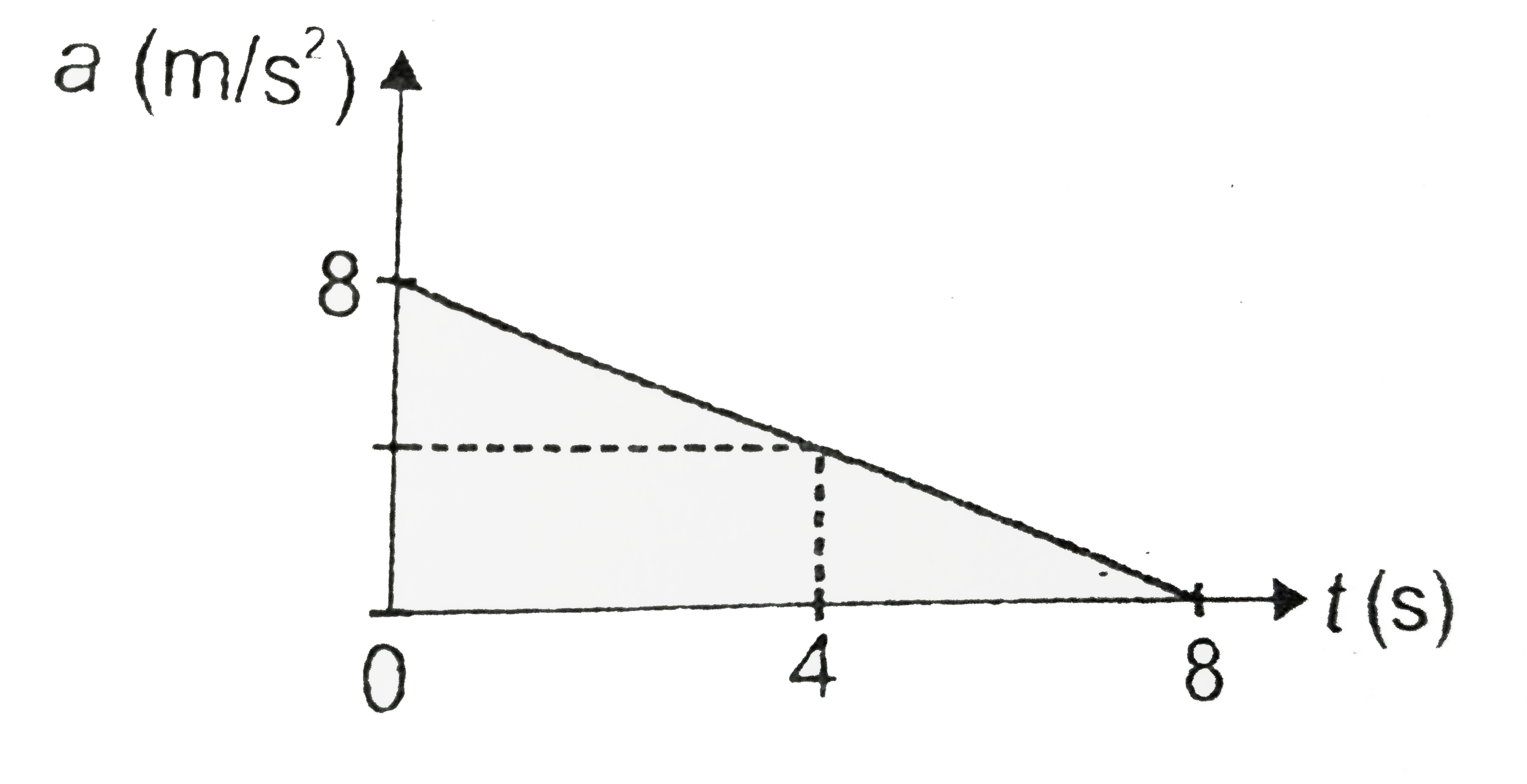
View SolutionA particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
View SolutionA particle starts moving with constant, velocity v=2ms, from position x=5m The position time graph will be
View SolutionA particle starts from rest with a time varying acceleration a=(2t−4). Here t is in second and a in m/s2
The velocity time graph of the particle is
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View Solution
