A particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
To solve the problem, we will use the equations of motion. The initial velocity (u) is 10 m/s, the acceleration (a) is -2 m/s², and we need to find the position (s) and velocity (v) at two different times: t = 5 s and t = 10 s.
1. Calculate the Position (s) at t = 5 s:
We use the second equation of motion:
s=ut+12at2
Substituting the values:
- u=10m/s
- a=−2m/s2
- t=5s
s=10×5+12×(−2)×(52)
s=50−12×2×25
s=50−25=25m
2. Calculate the Velocity (v) at t = 5 s:
We use the first equation of motion:
v=u+at
Substituting the values:
v=10+(−2)×5
v=10−10=0m/s
Summary for Part (i):
- Position at t = 5 s: 25 m
- Velocity at t = 5 s: 0 m/s
---
Part (ii): At t = 10 s
1. Calculate the Position (s) at t = 10 s:
Using the same second equation of motion:
s=ut+12at2
Substituting the values:
- u=10m/s
- a=−2m/s2
- t=10s
s=10×10+12×(−2)×(102)
s=100−12×2×100
s=100−100=0m
2. Calculate the Velocity (v) at t = 10 s:
Using the first equation of motion:
v=u+at
Substituting the values:
v=10+(−2)×10
v=10−20=−10m/s
Summary for Part (ii):
- Position at t = 10 s: 0 m
- Velocity at t = 10 s: -10 m/s
---
Final Answers:
- At t = 5 s: Position = 25 m, Velocity = 0 m/s
- At t = 10 s: Position = 0 m, Velocity = -10 m/s
We use the second equation of motion:
s=ut+12at2
Substituting the values:
- u=10m/s
- a=−2m/s2
- t=5s
s=50−12×2×25
s=50−25=25m
We use the first equation of motion:
v=u+at
Substituting the values:
v=10+(−2)×5
v=10−10=0m/s
- Position at t = 5 s: 25 m
- Velocity at t = 5 s: 0 m/s
Using the same second equation of motion:
s=ut+12at2
Substituting the values:
- u=10m/s
- a=−2m/s2
- t=10s
s=100−12×2×100
s=100−100=0m
Using the first equation of motion:
v=u+at
Substituting the values:
v=10+(−2)×10
v=10−20=−10m/s
- Position at t = 10 s: 0 m
- Velocity at t = 10 s: -10 m/s
- At t = 5 s: Position = 25 m, Velocity = 0 m/s
- At t = 10 s: Position = 0 m, Velocity = -10 m/s
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MOTION IN ONE DIMENSION EXERCISE - EXERCISE -2 (A)28videos
MOTION IN ONE DIMENSION
- BOOK - ICSECHAPTER - MOTION IN ONE DIMENSION EXERCISE - EXERCISE -2 (A) ( Multiple choice type: )5videos
MOTION IN ONE DIMENSION
- BOOK - ICSECHAPTER - MEASUREMENTS AND EXPERIMENTATION EXERCISE - TOPIC 2 SIMPLE PENDULUM (4 Marks Questions )1videos
MEASUREMENTS AND EXPERIMENTATION
- BOOK - ICSECHAPTER - PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREEXERCISE - Exercise -4(B)Numericals5videos
PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSURE
Similar Questions
A particle of mass 2kg starts moving in a straight line with an initial velocity of 2m/s at a constant acceleration of 2m/s2. Then rate of change of kinetic energy.
View SolutionA particle moving with uniform acceleration passes the point x=2m with velocity 20m/s at the instant t=0. Some time later it is observed at the point x=32m moving with velocity 10m/s.
(a) What is its acceleration?
(b) Find its position nd velocity at the instant t=8s.
(c) What is the distance traveled during the interval t=0 to 8s?View SolutionA body starts from rest and acquires a velocity 10 m s−1 in 2 s. Find the acceleration.
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionA particle starts moving in a straight line from rest with an acceleration (inm/s2) given by : a=12√x, where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m/s2 is .......m/s
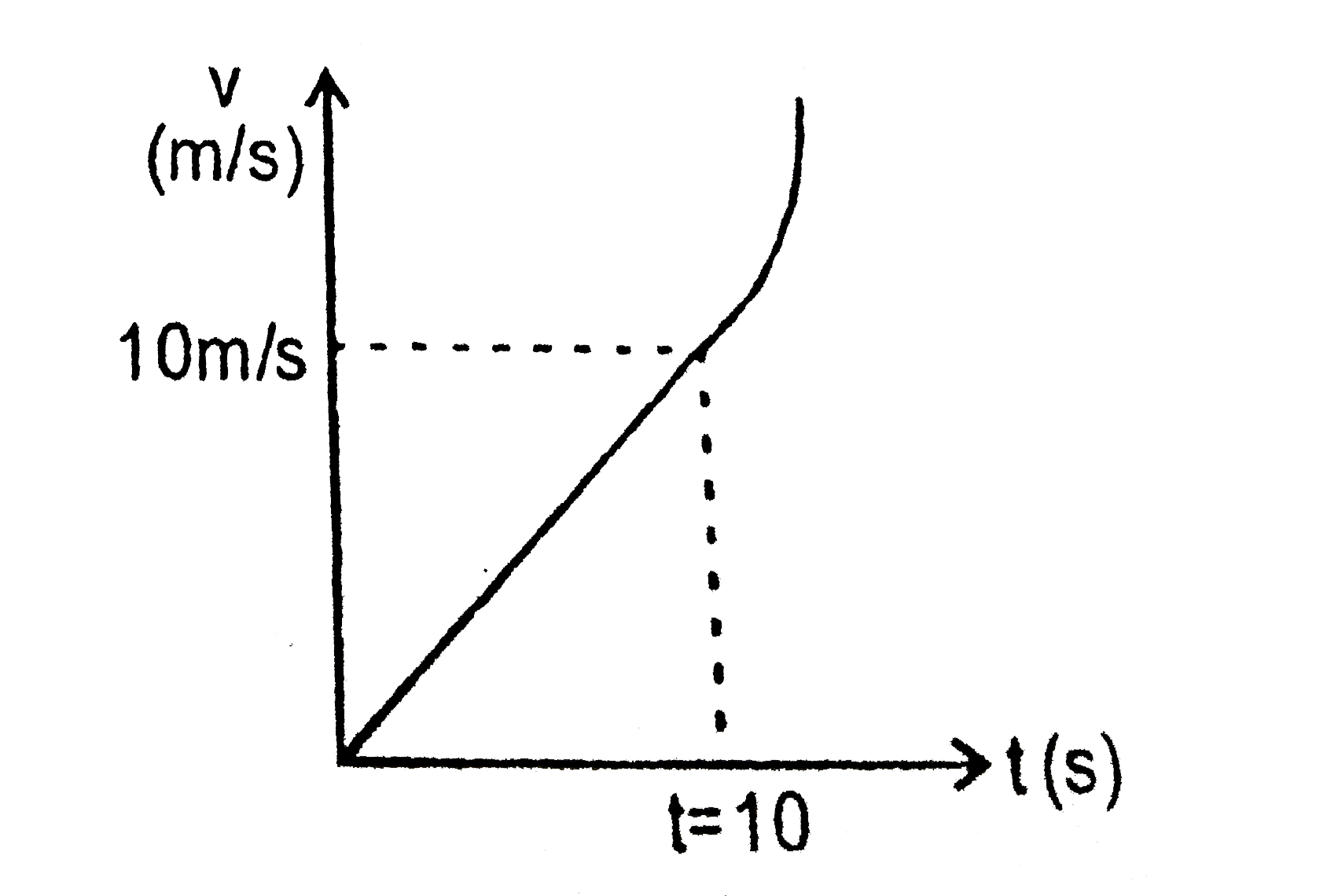
View SolutionA particle is moving in a straight line as :
a=1m/s20≤t≤10
a=2tt>10
where t is the time and a is the acceleration. If initial velocity of the particla is zero then :
 View Solution
View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionA particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View SolutionA particle starts from the origin at t = 0 s with a velocity of 10.0ˆj m/s and moves in plane with a constant acceleration of (8ˆi+2ˆj)ms−2. The y-coordinate of the particle in 2 sec is
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 View Solution
View Solution

