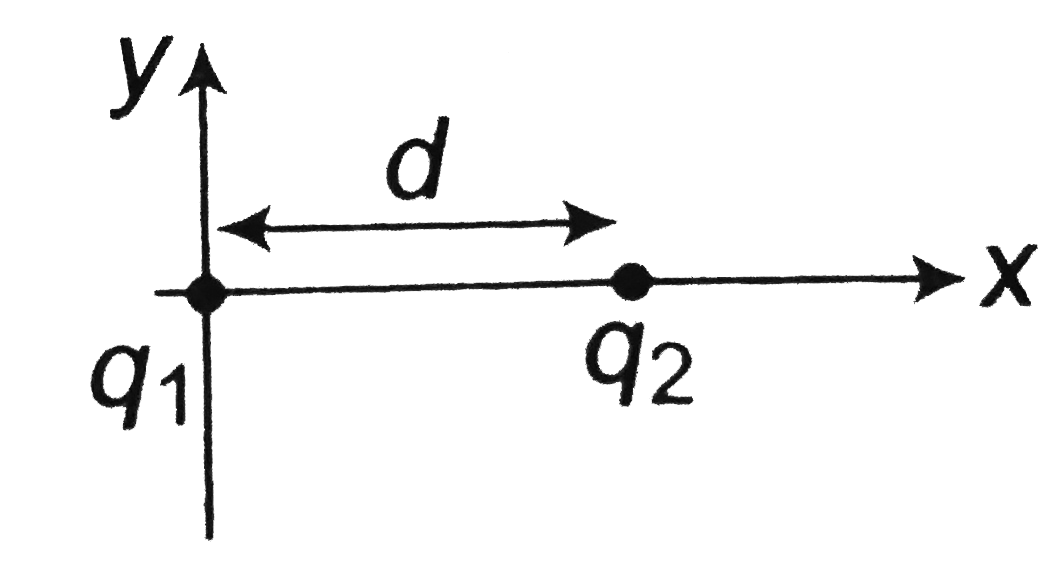
Two particles of charge q1 and q2 are separated by distance d as shown in figure. Chrage q1 is situarted at the origin. The net electirc field due to the particles is zero at x=d/4. With V=0 at infinity, the location of a point in terms of d on the x axis (other at infinfity) at which the elctrical potential due to the two particles is zero, is given by:
a.d/4
b.16d
c.−16d
d.no point on the axis
The correct Answer is:D
→E is zero in between the two charges. So both charges must have the same sign.
Therefore, electric potential cannot be zero anywhere on the axis.
Topper's Solved these Questions
Similar Questions
Two point charges Q and -Q/4 are separated by a distance x.

View SolutionTwo charge Q1=18μC and Q2=−2μC are separated by a distance R, and Q1 is on the left of Q2. The distance of the point where the net electric field is zero is
View Solutiontwo point charges + 16 q and -4q located at x=0 and x=L respectively. the location of a point on the x-axis from x=0, at which the net electric field due to these two charges is zero is
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionTwo point charges +8q and -2q are located at x=0 and x=L respectively. The location of a point on the x-axis from +8q at which the net electric field due to these two point charges is zero is
View SolutionTwo unlike charges of magnitude q are separated by a distance 2d. The potential at a point midway between them is
View Solution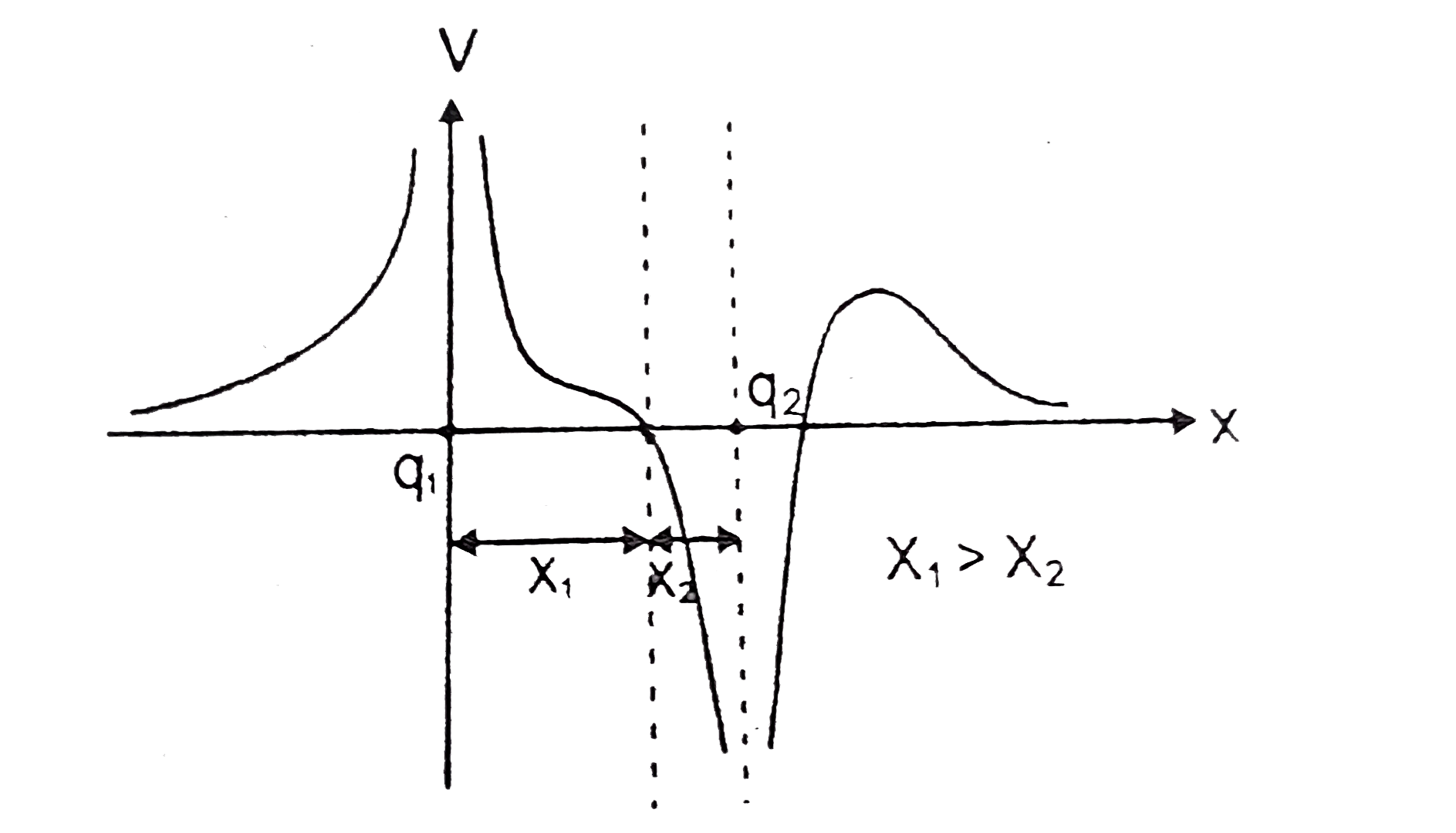
Two point charges (q1 and q2) are placed on x-axis, figure shows graph potential (V) on x-axis. With x-co-ordinate:
View SolutionTwo positive point charges q1=16μC and q2=4μC are separated in vacuum by a distance of 3.0m. Find the point on the line between the charges where the net electric field is zero.-
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View SolutionCharge 2qand−q are placed at (a,0)and(−a,0) as shown in the figure. The coordinates of the point at which electric field intensity is zero will be (x,0) where

View Solution
