Two positive point charges q1=16μC and q2=4μC are separated in vacuum by a distance of 3.0m. Find the point on the line between the charges where the net electric field is zero.-
The correct Answer is:A, B, C, D
To find the point on the line between two positive point charges q1=16μC and q2=4μC, separated by a distance of 3.0m, where the net electric field is zero, follow these steps:
Step 1: Understand the Configuration
We have two charges:
- q1=16μC located at point A.
- q2=4μC located at point B.
The distance between the charges is 3.0m.
Step 2: Define the Point of Interest
Let’s denote the point where the electric field is zero as point P. Assume that point P is located at a distance x from charge q2 (4 µC) and consequently at a distance 3−x from charge q1 (16 µC).
Step 3: Write the Electric Field Expressions
The electric field E due to a point charge is given by:
E=k⋅|q|r2
where k is Coulomb's constant, q is the charge, and r is the distance from the charge.
1. The electric field at point P due to q1 (16 µC) is:
E1=k⋅16×10−6(3−x)2
2. The electric field at point P due to q2 (4 µC) is:
E2=k⋅4×10−6x2
Step 4: Set the Electric Fields Equal
Since we want the net electric field at point P to be zero, we set the magnitudes of the electric fields equal to each other:
E1=E2
This gives us:
k⋅16×10−6(3−x)2=k⋅4×10−6x2
We can cancel k from both sides:
16×10−6(3−x)2=4×10−6x2
Step 5: Simplify the Equation
Now, we can simplify the equation:
16(3−x)2=4x2
Cross-multiplying gives:
16x2=4(3−x)2
Step 6: Expand and Rearrange
Expanding the right side:
16x2=4(9−6x+x2)
16x2=36−24x+4x2
Now, rearranging the equation:
16x2−4x2+24x−36=0
12x2+24x−36=0
Step 7: Simplify the Quadratic Equation
Dividing the entire equation by 12:
x2+2x−3=0
Step 8: Factor the Quadratic Equation
Factoring gives:
(x+3)(x−1)=0
Thus, x=−3 or x=1. Since x must be positive and within the range of 0 to 3 meters, we take:
x=1m
Step 9: Find the Distances from Each Charge
The distance from q2 (4 µC) to point P is 1m, and the distance from q1 (16 µC) to point P is:
3−x=3−1=2m
Final Answer
The point where the net electric field is zero is at a distance of 1m from charge q2 and 2m from charge q1.
---
We have two charges:
- q1=16μC located at point A.
- q2=4μC located at point B.
The distance between the charges is 3.0m.
Let’s denote the point where the electric field is zero as point P. Assume that point P is located at a distance x from charge q2 (4 µC) and consequently at a distance 3−x from charge q1 (16 µC).
The electric field E due to a point charge is given by:
E=k⋅|q|r2
where k is Coulomb's constant, q is the charge, and r is the distance from the charge.
E1=k⋅16×10−6(3−x)2
2. The electric field at point P due to q2 (4 µC) is:
E2=k⋅4×10−6x2
Since we want the net electric field at point P to be zero, we set the magnitudes of the electric fields equal to each other:
E1=E2
This gives us:
k⋅16×10−6(3−x)2=k⋅4×10−6x2
We can cancel k from both sides:
16×10−6(3−x)2=4×10−6x2
Now, we can simplify the equation:
16(3−x)2=4x2
Cross-multiplying gives:
16x2=4(3−x)2
Expanding the right side:
16x2=4(9−6x+x2)
16x2=36−24x+4x2
Now, rearranging the equation:
16x2−4x2+24x−36=0
12x2+24x−36=0
Dividing the entire equation by 12:
x2+2x−3=0
Factoring gives:
(x+3)(x−1)=0
Thus, x=−3 or x=1. Since x must be positive and within the range of 0 to 3 meters, we take:
x=1m
The distance from q2 (4 µC) to point P is 1m, and the distance from q1 (16 µC) to point P is:
3−x=3−1=2m
The point where the net electric field is zero is at a distance of 1m from charge q2 and 2m from charge q1.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 55videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 64videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Two point charges of 5μC and 20μC are separated by a distance of 2m. Find the point on the line joining them at which electric field intensity is zero.
View SolutionTwo charge Q1=18μC and Q2=−2μC are separated by a distance R, and Q1 is on the left of Q2. The distance of the point where the net electric field is zero is
View SolutionTwo point charges 4μCand−2μC are separated by a distance of 1m in air. Calculate at what point on the line joining the two charges is the electric potential zero ?
View SolutionThe position of the point where the net electric field will be zero is
 View Solution
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View SolutionTwo point charges qA=3μCandqB=−3μC are located 20cm apart in vacuum. What is the electric field at the mid point of the line joining the two charges.
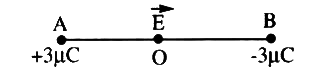 View Solution
View SolutionTwo point charges Q and -Q/4 are separated by a distance x.
 View Solution
View SolutionTwo point charges +Q and -Q are separated by a certain distance. The resultant electric field is parallel to the line joining the charges at the points
View SolutionTwo point charges of +16μCand−9μC are placed 8 cm apart in air. Determine the position of the point at which the resultant electric field is zero.
View SolutionCharges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
View Solution

