Two particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end and is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
To calculate the angular momentum of the particle at the end of the rod (let's call it particle B) with respect to the particle at the center of the rod (let's call it particle A), we can follow these steps:
Step 1: Identify the system
We have two particles of mass m each attached to a light rod of length d. One particle (A) is located at the center of the rod, and the other particle (B) is at the free end of the rod. The rod is fixed at one end and is rotating in a plane with an angular speed ω.
Step 2: Determine the distances from the center of rotation
- The distance from the fixed end (point O) to particle A is d2.
- The distance from the fixed end to particle B is d.
Step 3: Calculate the linear velocities of the particles
Using the formula for linear velocity v=r⋅ω:
- For particle A (at distance d2):
vA=d2⋅ω
- For particle B (at distance d):
vB=d⋅ω
Step 4: Find the relative velocity of particle B with respect to particle A
The relative velocity vBA is given by:
vBA=vB−vA
Substituting the values:
vBA=(d⋅ω)−(d2⋅ω)=d⋅ω−d2⋅ω=d2⋅ω
Step 5: Determine the distance from particle A to particle B
The distance RBA from particle A to particle B is simply the length of the rod:
RBA=d
Step 6: Calculate the angular momentum of particle B with respect to particle A
The angular momentum L is given by the formula:
L=m⋅vBA⋅RBA
Substituting the values:
L=m⋅(d2⋅ω)⋅d=m⋅d22⋅ω
Final Result
Thus, the angular momentum of particle B with respect to particle A is:
L=m⋅d2⋅ω2
We have two particles of mass m each attached to a light rod of length d. One particle (A) is located at the center of the rod, and the other particle (B) is at the free end of the rod. The rod is fixed at one end and is rotating in a plane with an angular speed ω.
- The distance from the fixed end (point O) to particle A is d2.
- The distance from the fixed end to particle B is d.
Using the formula for linear velocity v=r⋅ω:
- For particle A (at distance d2):
vA=d2⋅ω
- For particle B (at distance d):
vB=d⋅ω
The relative velocity vBA is given by:
vBA=vB−vA
Substituting the values:
vBA=(d⋅ω)−(d2⋅ω)=d⋅ω−d2⋅ω=d2⋅ω
The distance RBA from particle A to particle B is simply the length of the rod:
RBA=d
The angular momentum L is given by the formula:
L=m⋅vBA⋅RBA
Substituting the values:
L=m⋅(d2⋅ω)⋅d=m⋅d22⋅ω
Thus, the angular momentum of particle B with respect to particle A is:
L=m⋅d2⋅ω2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
Two small balls A and B each of mass m, are attached tightly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed ω. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View Solution
Knowledge Check
A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed ω. If the angular momentum of the system. calculated about O and P are denoted. by →LOand→LP respectively, then.
 A→LOand→LP do not vary with time.B→LO varies with time while →LP remains constantC→LO remains constant while →LP varies with timeD→LOand→LP both vary with time
A→LOand→LP do not vary with time.B→LO varies with time while →LP remains constantC→LO remains constant while →LP varies with timeD→LOand→LP both vary with time

A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA particle is attached to an end of a rigid rod. The other end of the rod is hunged and the rod rotates always remaining horizontal. Its angular speed is increasing at contant rate. The mass of the particle is m . The force exerted by the rod on the particle is →F , then:
View SolutionA particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
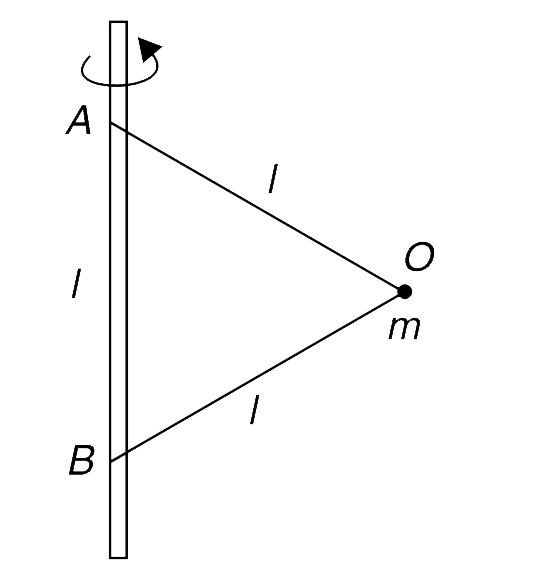
View SolutionA particle, held by a string whose other end is attached to a fixed point C, moves in a circle on a horizontal frictionless surface. If the string is cut, the angular momentum of the particle about the point C
View SolutionTwo particles of masses m1andm2 are joined by a light rigid rod of length r. The system rotates at an angular speed ω about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is L=μr2ω where μ is the reduced mass of the system defined as μ=m1m2m1+m2
View SolutionA particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical ciorcular path about its other end. The minimum speed of the particle at its highest point must be
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is

View Solution
