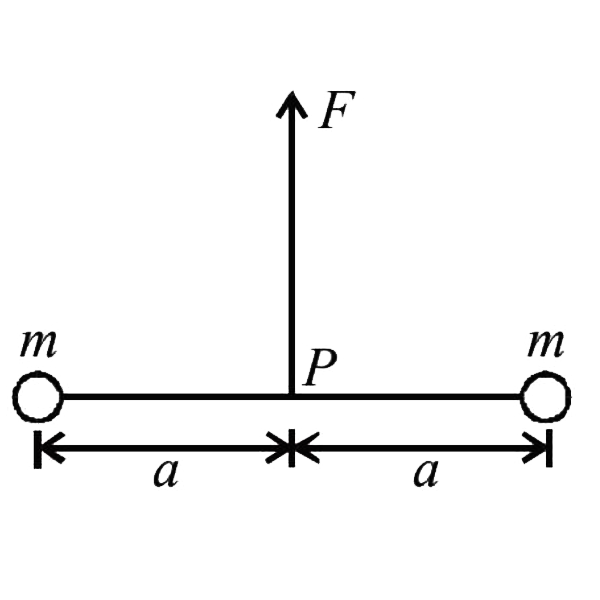
Two particles of mass 'm' each are tied at eh ends of a light string of length '2a' The whole system is kept on frictionless horizontal surface with the string held tight so that each mass is at a distance 'a' from the centre P (as shown in figure). Now the mid point of the string is pulled vertically upwards with a small but constant force F As a result, the particles move towards each other on the surface the magnitude of acceleration, when the separation between them becomes 2x is:
The correct Answer is:B
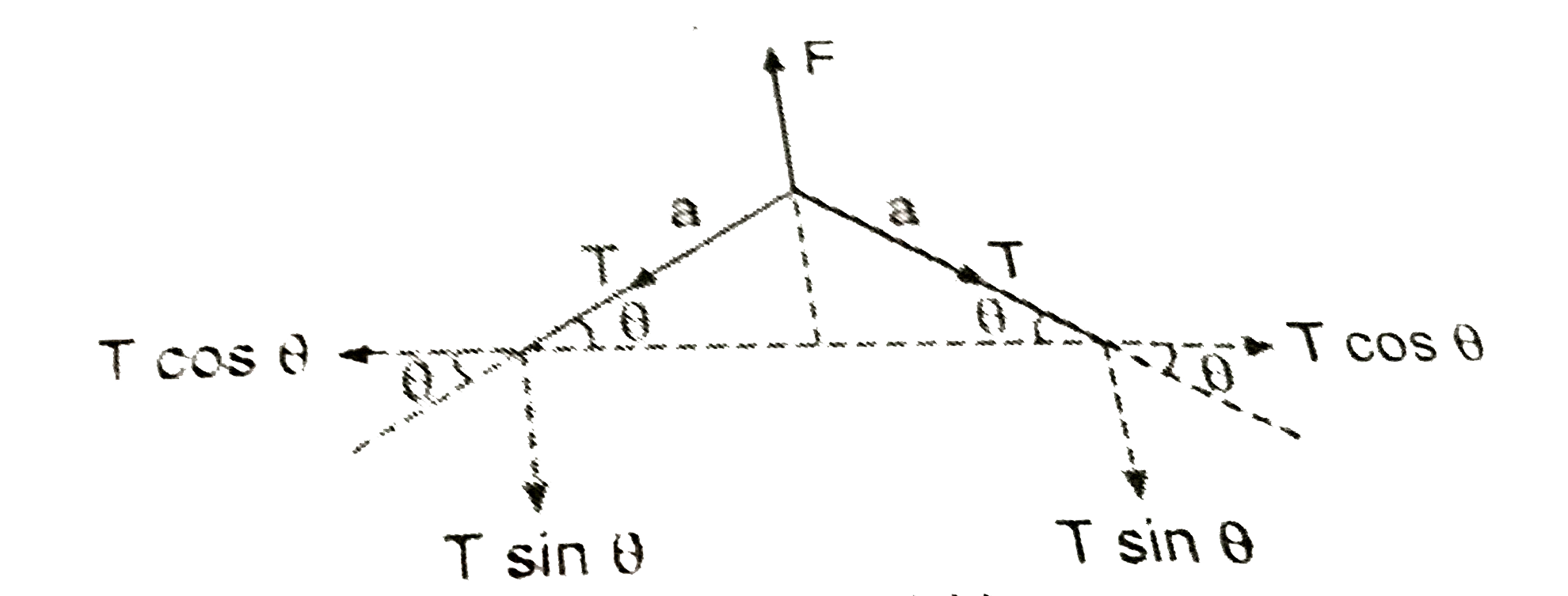
From the figure
….(i)
….(ii)
Dividing eqn (ii) by eqn (i)
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason
4 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
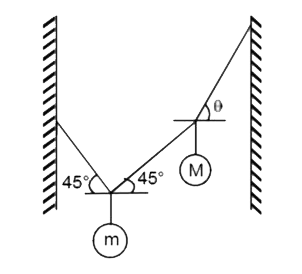
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibruim, then
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View Solution
Knowledge Check
Two particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
 AF2m/(√a2−x2)BF2mx√a2−x2CF2mxaDF2m√a2−x2x
AF2m/(√a2−x2)BF2mx√a2−x2CF2mxaDF2m√a2−x2xTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that, each mass is at a distance 'a' from the center P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is :
 AF2ma√a2−x2BF2mx√a2−x2CF2mxaDF2m√a2−x2x
AF2ma√a2−x2BF2mx√a2−x2CF2mxaDF2m√a2−x2xTwo masses M and m are connected by a weightless string. They are pulled by a force F on a frictionless horizontal surface. The tension in the string will be
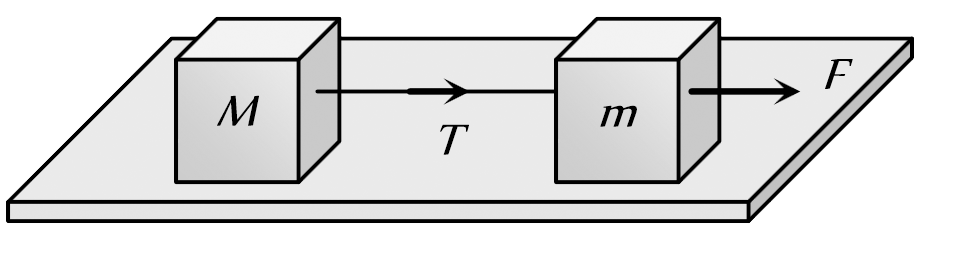 AFMm+MBFM+mCFMmDFmM+m
AFMm+MBFM+mCFMmDFmM+m
Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then
View SolutionTwo block of mass 5 kg and 10 kg respectively are connected by a massless string as shown in the figure. The whole system is kept on a frictionless surface. A force of 50 N is applied horizontally as shown in the figure. The tension T in the string will be
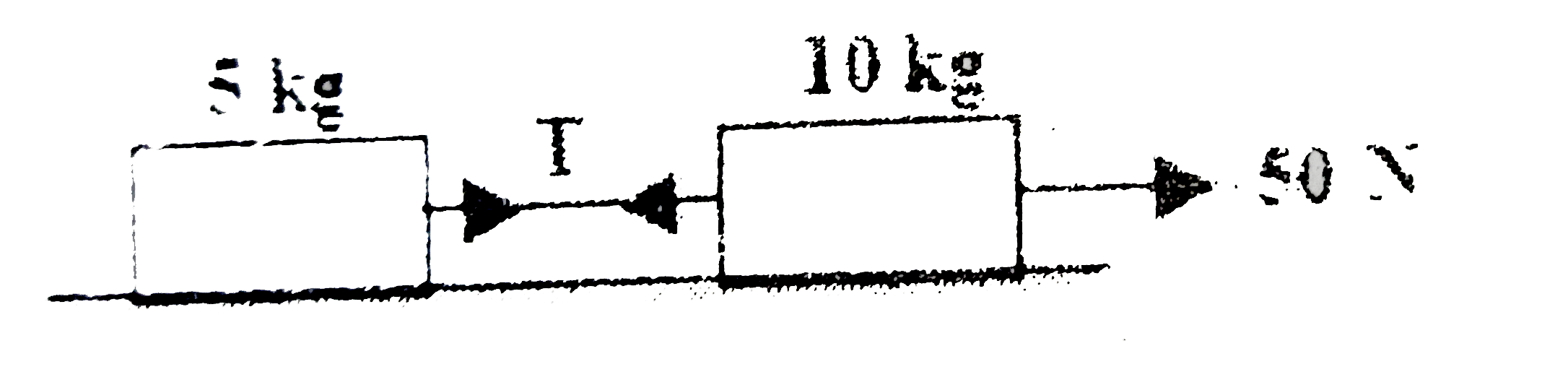
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
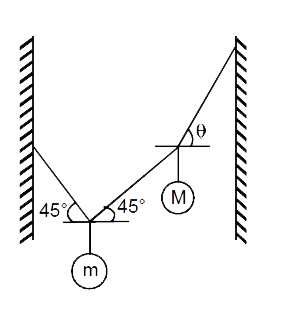
View Solution
