Two particles of masses $m_{1} and m_{2}$ are joined y a light rigid rod of length r. The system rotates at an angular speed $ω$ about an axis through the centre of mass of the systemand perpendicular to the rod. Shwo thast the angular momentum of the system $i s L = μ r^{2} ω w h e r e μ$ is the reduced mass of the system defined as $μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}}$

$μ = m_{1} + m_{2}$

$μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}}$

$μ = \sqrt{m_{1} m_{2}}$

$μ = \frac{m_{1} + m_{2}}{m_{1} m_{2}}$

Video Solution

Text Solution

Verified by Experts

Let $x_{1}$ and $x_{2}$ are the distances of particles from centre of mass as shown in figure.

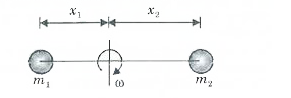
$x_{1} = \frac{m_{2} l}{(m_{1} + m_{2})}$ and $x_{2} = \frac{m_{1} l}{(m_{1} + m_{2})}$
Moment of inertia of the system about axis passing through the centre of mass can be written as follows:
$I = m_{1} {[\frac{m_{2} l}{(m_{1} + m_{2})}]}^{2} + m_{2} {[\frac{m_{1} l}{(m_{1} + m_{2})}]}^{2}$
$\Rightarrow I = [\frac{m_{1} m_{2}}{m_{1} + m_{2}}] l^{2}$
Angular momentum can be written as
$L = I ω \Rightarrow L = (\frac{m_{1} m_{2}}{m_{1} + m_{2}}) l^{2} ω = μ l^{2} ω$ Comparing it with the given result we get $μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}}$ .

Updated on:21/07/2023

Two balls of masses $m$ and $2 m$ are attached to the ends of a light rod of length $L$ . The rod rotates with an angular speed $ω$ about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
A $\frac{2}{3} m ω L^{2}$
B $\frac{1}{3} ω^{2} L m$
C $\frac{2}{3} ω^{2} L m$
D $\frac{1}{3} L m$
Two particles of masses 2 kg and 3 kg are separated by 5 m. Then moment of inertia of the system about an axis passing through the centre of mass of the system and perpendicular to the line joining them is
A $10 k g m^{2}$
B $20 k g m^{2}$
C $30 k g m^{2}$
D $40 k g m^{2}$
Two spheres each mass M and radius R are connected with massless rod of length 2R . Then moment of inertia of the system about an axis passing through the centre of one of sphere and perpendicular to the rod will be
A $\frac{21}{5} M R^{2}$
B $\frac{23}{5} M R^{2}$
C $\frac{22}{5} M R^{2}$
D $\frac{24}{5} M R^{2}$