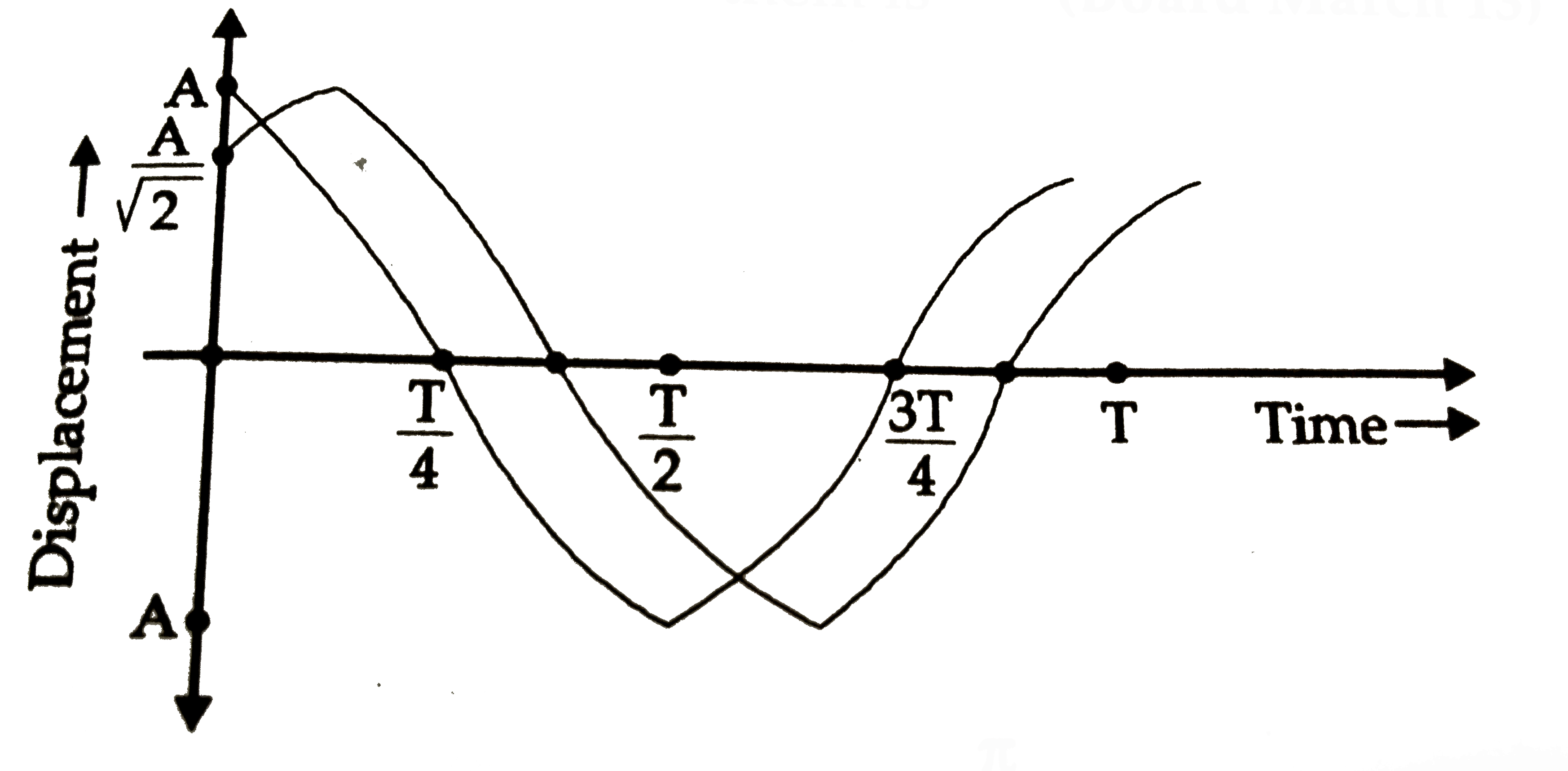
Two particles perform linear simple harmonic motion along the same path of length 2 A and period T as shown in the graph below. The phase difference between them is
Zero rad
π4 rad
π2rad
3π4rad
The correct Answer is:B
From the graph we find that when the particle P is at A or extreme position, particle Q is at a dis"tan"ce of A√2 from the mean position. U"sin"g x=Asin(ωt)andx=A√2, we get A√2=Asin(ωt)
∴sin(ωt)=1√2=sin(π4)or(ωt)=π4 for Q while for P, phase =π2
∵A=Asin(ωt1)∴ωt1=1
∴1=sin(π2)=sin(ωt1)
Phase (ωt1)=π2
∴ Phase difference =π2−π4=π4 radian
Topper's Solved these Questions
Similar Questions
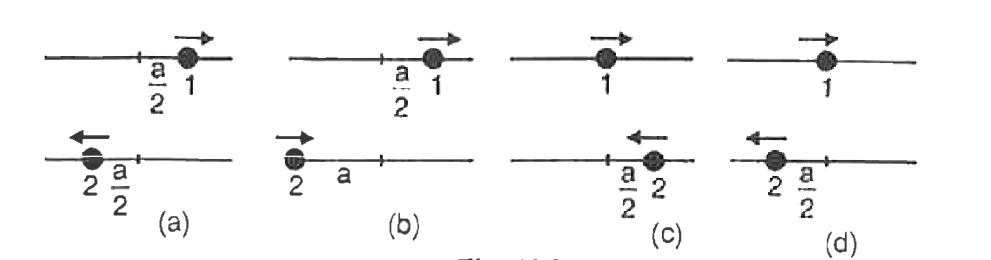
Find the phase difference between two particles executing simple harmonic motion with the same frequency if they are found inn the states shown in the figures at four different points of time.
View SolutionA particle executes a linear simple harmonic motion of amplitude 20 cm and time period 4 s. The minimum time period required for the particle to move between two points located at 10 cm on either side of equilibrium position is t seconds, then compute 3t + 2 .
View Solution
Knowledge Check
Two bodies performing S.H.M. have same amplitude and frequency. Their phases at a certain instant are as shown in the figure. The phase difference between them is
_E01_002_Q01.png) A116πBπC53πD35π
A116πBπC53πD35πTwo simple harmonic motions are represented by y1=10sinωt and y2=15cosωt. The phase difference between them is
AZeroBπ6 radianCπ4 radianDπ2 radianTwo particles A and B execute simple harmonic motions of period T and 5T/4. They start from mean position. The phase difference between them when the particle A complete an oscillation will be
Aπ/2BzeroC2π/5Dπ/4
Two particles A and B execute simple harmonic motions of period T and 5T/4. They start from mean position. The phase difference between them when the particle A complete an oscillation will be
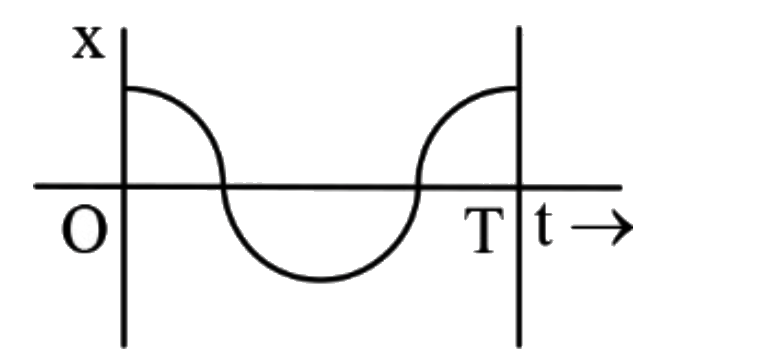
View SolutionA body is performing simple harmonic motion of amplitude A and time period T. The figure shown position-time graph of the body . At any time t, acceleration of the body is f, then which of the following graphs is/are appropriate?
View SolutionTwo linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is π2. The resultant path followed by the particle is
View SolutionThe phase (at a time t) of a particle in simple harmonic motion tells
View SolutionA mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
View Solution
