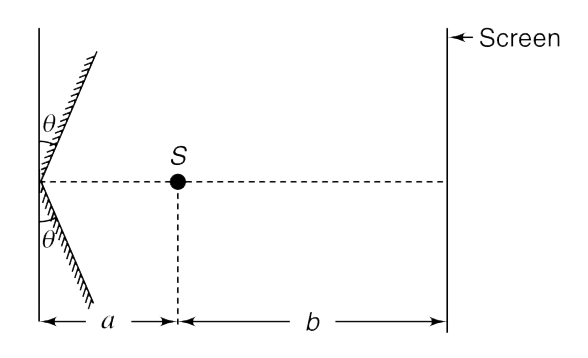
Two plane mirrors, a source S of light, emitting wavelengths ofλ1=4000∘A andλ2=5600∘Aand a screen are arranged as shown in figure. The angle θ shown is 0.05 radian and distance a and b are 1 cm and 38 cm respectively.
(a) Find the fringe width of interference pattern formed on screen by the blue light.
(b) Calculate the distance of first black line from central bright fringe.
(c) Find the distance between two black lines which are nearest to the central bright fringe.
The correct Answer is:(a)80μm (b)280μm(c)560μm
Step by step video, text & image solution for Two plane mirrors, a source S of light, emitting wavelengths of lambda_(1) = 4000overset(@)A" and" lambda_(2) = 5600overset(@)Aand a screen are arranged as shown in figure. The angle theta shown is 0.05 radian and distance a and b are 1 cm and 38 cm respectively. (a) Find the fringe width of interference pattern formed on screen by the blue light. (b) Calculate the distance of first black line from central bright fringe. (c) Find the distance between two black lines which are nearest to the central bright fringe. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
_E01_104_Q01.png)
Two plane mirrors, a source S of light, wmitting monochromatic rays of wavelength λ and a screen are arranged as shown in figure. If angle θ is very small, calculate fringe width of the interference pattern formed by reflected rays.
View SolutionIn Y.D.S.E., slits are at a distance of 0.5 mm and light of wavelength λ is used. Determine the value of λ if interference pattern is formed at a distance 1.2 m away and third dark fringe is at a distance of 1.2 cm from the central fringe.
View Solution
Knowledge Check
Two sources give interference pattern which is observed on a screen, D distance apart from the sources. The fringe width is 2 w . If the distance D is now doubled, the fringe width will
ABecome w /2BRemain the sameCBecome wDBecome 4 wIn Yonung's double-slit experiment, two slits which are separated by 1.2 mm are illuminated with a monochromatic light of wavelength 6000Å The interference pattern is observed on a screen placed at a distance of 1 m from the slits. Find the number of bright fringes formed over 1 cm width on the screen.
A25B12C15D20In Young's double slit experiment, the distance between sources is 1mm and distance between the screen and source is 1 m . If the fringe width on the screen is 0.06cm , then λ=
A6000ÅB4000ÅC1200ÅD2400Å
In Young's experiment, interference pattern is obtained on a screen at a distance of 1m from slits separated by 0.05cm and illuminated by sodium light of wavelength 5893Å. Calculate distance between 4th bright fringe on one side and 3rd bright fringe on other side of central bright fringe.
View SolutionWhat is interference ? In Young's double-slit experiment, show that the fringe width β for interference fringes is β=λDd
Where D is the distance of the screen from the slit, d is the distance between two slits and λ is the wavelength of light used.
View SolutionIn Y.D.S.E., light of wavelength 5500Å is used. If the slits are at a distance of 10−3m and interference pattern is formed at a distance of 100 cm.
Calculate the distance between central fringe and second dark fringe.
View SolutionIn a biprism experiment, the distance between the first and eleventh bright fringes formed by light of wavelength λ is 1.8×10−3m. If the light is replaced by one width wavelength 0.8λ, find the distance between the first and sixteenth bright fringes.
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View Solution
