Two point charge each +3 µC are placed along the diameter of a circle of radius 15 cm. Calculate the ectric potential at the ends of perpendicular diameter
To solve the problem of calculating the electric potential at the ends of a perpendicular diameter of a circle with two point charges of +3 µC each placed along its diameter, we can follow these steps:
1. Understand the Configuration:
- We have two point charges, each of +3 µC, placed at the ends of a diameter of a circle with a radius of 15 cm.
- The points where we need to calculate the electric potential are the ends of a perpendicular diameter.
2. Convert Units:
- The radius of the circle is given as 15 cm. We need to convert this to meters for our calculations:
R=15cm=0.15m
3. Identify the Distance from Charges:
- The distance from each charge to the ends of the perpendicular diameter can be calculated using the Pythagorean theorem. Since the diameter is perpendicular, the distance r from each charge to the point where we are calculating the potential is:
r=√R2+R2=√(0.15)2+(0.15)2=√0.0225+0.0225=√0.045≈0.21m
4. Calculate the Electric Potential from Each Charge:
- The electric potential V due to a point charge is given by the formula:
V=k⋅Qr
- Where k is Coulomb's constant (8.99×109N m2/C2), Q is the charge, and r is the distance from the charge to the point of interest.
5. Calculate V1 and V2:
- For the first charge:
V1=(9×109)⋅(3×10−6)0.21≈128.57×103V
- For the second charge (since both charges are identical and at the same distance):
V2=(9×109)⋅(3×10−6)0.21≈128.57×103V
6. Calculate the Total Electric Potential:
- The total electric potential at point A (and similarly at point B due to symmetry) is:
VA=V1+V2=128.57×103+128.57×103=257.14×103V
- This can be expressed as:
VA=2.57×105V
7. Conclusion:
- The electric potential at both ends of the perpendicular diameter is:
VA=VB=2.57×105V
- We have two point charges, each of +3 µC, placed at the ends of a diameter of a circle with a radius of 15 cm.
- The points where we need to calculate the electric potential are the ends of a perpendicular diameter.
- The radius of the circle is given as 15 cm. We need to convert this to meters for our calculations:
R=15cm=0.15m
- The distance from each charge to the ends of the perpendicular diameter can be calculated using the Pythagorean theorem. Since the diameter is perpendicular, the distance r from each charge to the point where we are calculating the potential is:
r=√R2+R2=√(0.15)2+(0.15)2=√0.0225+0.0225=√0.045≈0.21m
- The electric potential V due to a point charge is given by the formula:
V=k⋅Qr
- Where k is Coulomb's constant (8.99×109N m2/C2), Q is the charge, and r is the distance from the charge to the point of interest.
- For the first charge:
V1=(9×109)⋅(3×10−6)0.21≈128.57×103V
- For the second charge (since both charges are identical and at the same distance):
V2=(9×109)⋅(3×10−6)0.21≈128.57×103V
- The total electric potential at point A (and similarly at point B due to symmetry) is:
VA=V1+V2=128.57×103+128.57×103=257.14×103V
- This can be expressed as:
VA=2.57×105V
- The electric potential at both ends of the perpendicular diameter is:
VA=VB=2.57×105V
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (2 MARKS)
59 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (3 MARKS )
23 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
Knowledge Check
What is the diameter of the circle having 3 cm radius?
A6 cmB12 cmC1.5 cmD8 cmFour point charges each +q is placed on the circumference of a circle of diameter 2d in such a way that they form a square. The potential at the centre is
A0B4kqdC4dqDq4dTwo sources of sound are placed along the diameter of a circle of radius R(R>>41). How many minima will be heard as one moves along the perimeter of circle.
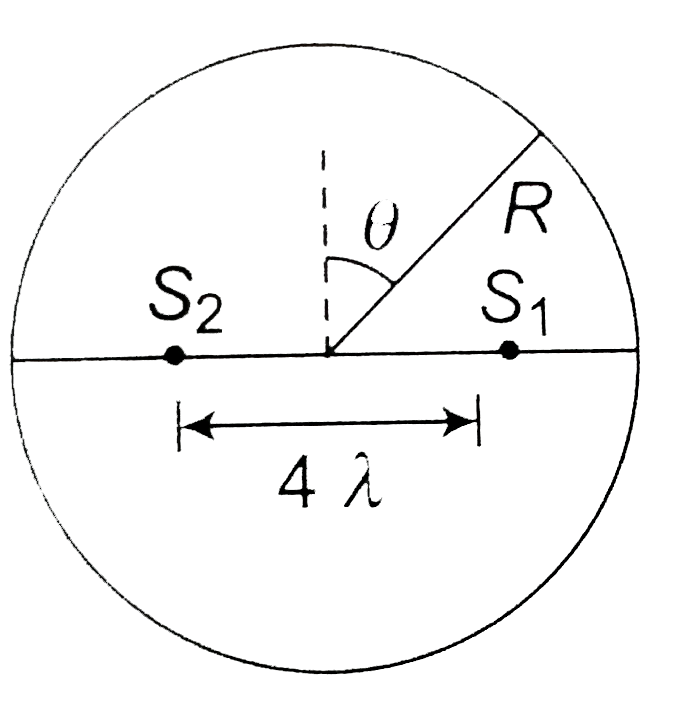 A12B16C4D20
A12B16C4D20
3. The diameter of a circle is 21 cm. Find the length of its radius.
View SolutionDraw a circle of radius 6 cm.Measure the diameter and verify that length of diameter is 12 cm
View SolutionThe tangents drawn at the end points of the diameter of a circle will be
View SolutionIf one end of the diameter of a circle is (3, 4) which touches the x-axis then the locus of other end of the diameter of the circle is
View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
View Solution
