Two points nonochromatic and coherent sources of light of wavelength each are placed as shown in figure. The initial phase difference between the sources is zero O. . Mark the correct statement(s).
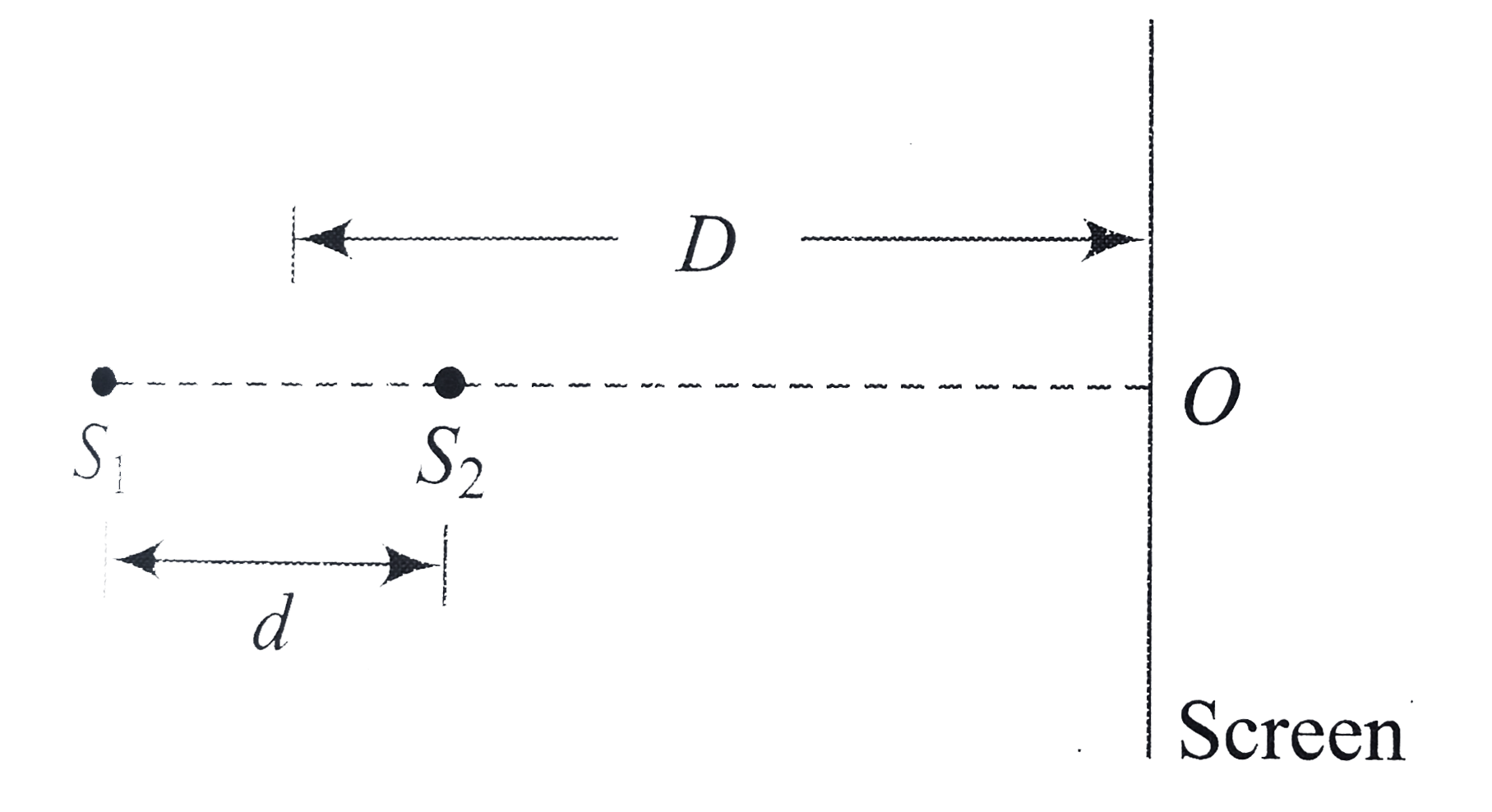
If will be minima.
If , only one maxima can be observed on screen.
If then total 10 minimas would be there on screen.
If , then intensity at O would be maximum.
The correct Answer is:D
Path difference,
So, if will be a minima.
If will be maxima.
If will be minima and hence intensity is minimum.
If then total 10 minimas can be observed on screen, 5 above and 5 below O, which correspond to
Topper's Solved these Questions
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - NCERT EXEMPLAR PROBLEMS
5 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - ASSERTION & REASON CORNER
15 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion And Reason
15 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Four monochromatic and coherent sources of light, emitting waves in phase of wavelength λ, are placed at the points x = 0, d 2d and 3d on the x-axis. Then
View SolutionTwo coherent sources of light interfere and produce fringe pattern on a screen . For central maximum phase difference between two waves will be
View SolutionTwo identical radiators have a separation of d=λ/4 where λ is the wavelength of the waves emitted by either source. The initial phase difference between the sources is π/4. Then the intensity on the screen at a distant point situated at an angle θ=30∘ from the radiators is (here I0 is intensity at that point due to one radiator alone)
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is

View SolutionA sound source emits two sinusoidal sound waves, both of wavelength λ, along paths A and B as shown in figure.The sound travelling along path B is reflected from five surfaces as shown and then merges at point Q, producing minimum intensity at that point.The minimum value of d in terms of λ is :

View SolutionA parallel beam of light of wavelength λ passes through a slit of width d. The transmitted light is collected on a screen D aways (D>>d). Find the distance between the two second order minima.
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent sources each emitting light of intensity I0 Interfere, in a medium at a point, where phase different between them is 2π3. Then, the resultant intensity at that point would be.
View Solution
