Four monochromatic and coherent sources of light, emitting waves in phase of wavelength λ, are placed at the points x = 0, d 2d and 3d on the x-axis. Then
point having |x|>>d appear dark if d=λ/4
point having |x|>>d appear dark if d=λ/8
point having |x|>>d appear maximum bright dark if d=λ/4
point having |x|>>d appear maximum bright dark if d=λ/8
The correct Answer is:A
Step-by-Step Solution:
1. Identify the Sources:
The sources are located at:
- Source 1 at x=0
- Source 2 at x=d
- Source 3 at x=2d
- Source 4 at x=3d
2. Determine the Path Difference:
To find the interference pattern, we need to calculate the path difference between the waves coming from these sources to a point P on the screen. Let’s denote the distance from the point P to the sources as follows:
- Distance from Source 1 to P: r1
- Distance from Source 2 to P: r2
- Distance from Source 3 to P: r3
- Distance from Source 4 to P: r4
The path differences between pairs of sources can be calculated as:
- Path difference between Source 1 and Source 2: Δr12=r2−r1
- Path difference between Source 1 and Source 3: Δr13=r3−r1
- Path difference between Source 1 and Source 4: Δr14=r4−r1
- Path difference between Source 2 and Source 3: Δr23=r3−r2
- Path difference between Source 2 and Source 4: Δr24=r4−r2
- Path difference between Source 3 and Source 4: Δr34=r4−r3
3. Condition for Constructive and Destructive Interference:
For constructive interference (bright fringes), the path difference must be an integer multiple of the wavelength λ:
Δr=nλ(n=0,1,2,…)
For destructive interference (dark fringes), the path difference must be an odd multiple of half the wavelength:
Δr=(n+12)λ(n=0,1,2,…)
4. Analyze the Interference Pattern:
Since the sources are coherent and in phase, we can expect an interference pattern with alternating bright and dark fringes. The positions of these fringes will depend on the path differences calculated above.
5. Final Conclusion:
The resulting interference pattern will show a series of bright and dark fringes on the screen, with the positions determined by the conditions for constructive and destructive interference.
The sources are located at:
- Source 1 at x=0
- Source 2 at x=d
- Source 3 at x=2d
- Source 4 at x=3d
To find the interference pattern, we need to calculate the path difference between the waves coming from these sources to a point P on the screen. Let’s denote the distance from the point P to the sources as follows:
- Distance from Source 1 to P: r1
- Distance from Source 2 to P: r2
- Distance from Source 3 to P: r3
- Distance from Source 4 to P: r4
- Path difference between Source 1 and Source 2: Δr12=r2−r1
- Path difference between Source 1 and Source 3: Δr13=r3−r1
- Path difference between Source 1 and Source 4: Δr14=r4−r1
- Path difference between Source 2 and Source 3: Δr23=r3−r2
- Path difference between Source 2 and Source 4: Δr24=r4−r2
- Path difference between Source 3 and Source 4: Δr34=r4−r3
For constructive interference (bright fringes), the path difference must be an integer multiple of the wavelength λ:
Δr=nλ(n=0,1,2,…)
For destructive interference (dark fringes), the path difference must be an odd multiple of half the wavelength:
Δr=(n+12)λ(n=0,1,2,…)
Since the sources are coherent and in phase, we can expect an interference pattern with alternating bright and dark fringes. The positions of these fringes will depend on the path differences calculated above.
The resulting interference pattern will show a series of bright and dark fringes on the screen, with the positions determined by the conditions for constructive and destructive interference.
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) More than one correct answer type questions
4 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Linked Comprehension type questions
6 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
Four monochromatic and coherent sources of light emitting waves in phase at placed on y axis at y = 0, a, 2a and 3a. If the intensity of wave reaching at point P far away on y axis from each of the source is almost the same and equal to I0, then the resultant intensity at P for a=λ8 is nI0. The value of [n] is.
Here [] is greatest integer funciton.
View SolutionTwo monochromatic (wavelength = a/5) and coherent sources of electromagnetic waves are placed on the x-axis at the points (2a,0) and (-a,0). A detector moves in a circle of radius R(gtgt2a) whose centre is at the origin. The number of maxima detected during one circular revolution by the detector are
View Solution
Knowledge Check
Two points nonochromatic and coherent sources of light of wavelength λ each are placed as shown in figure. The initial phase difference between the sources is zero O. (d>>d). Mark the correct statement(s).
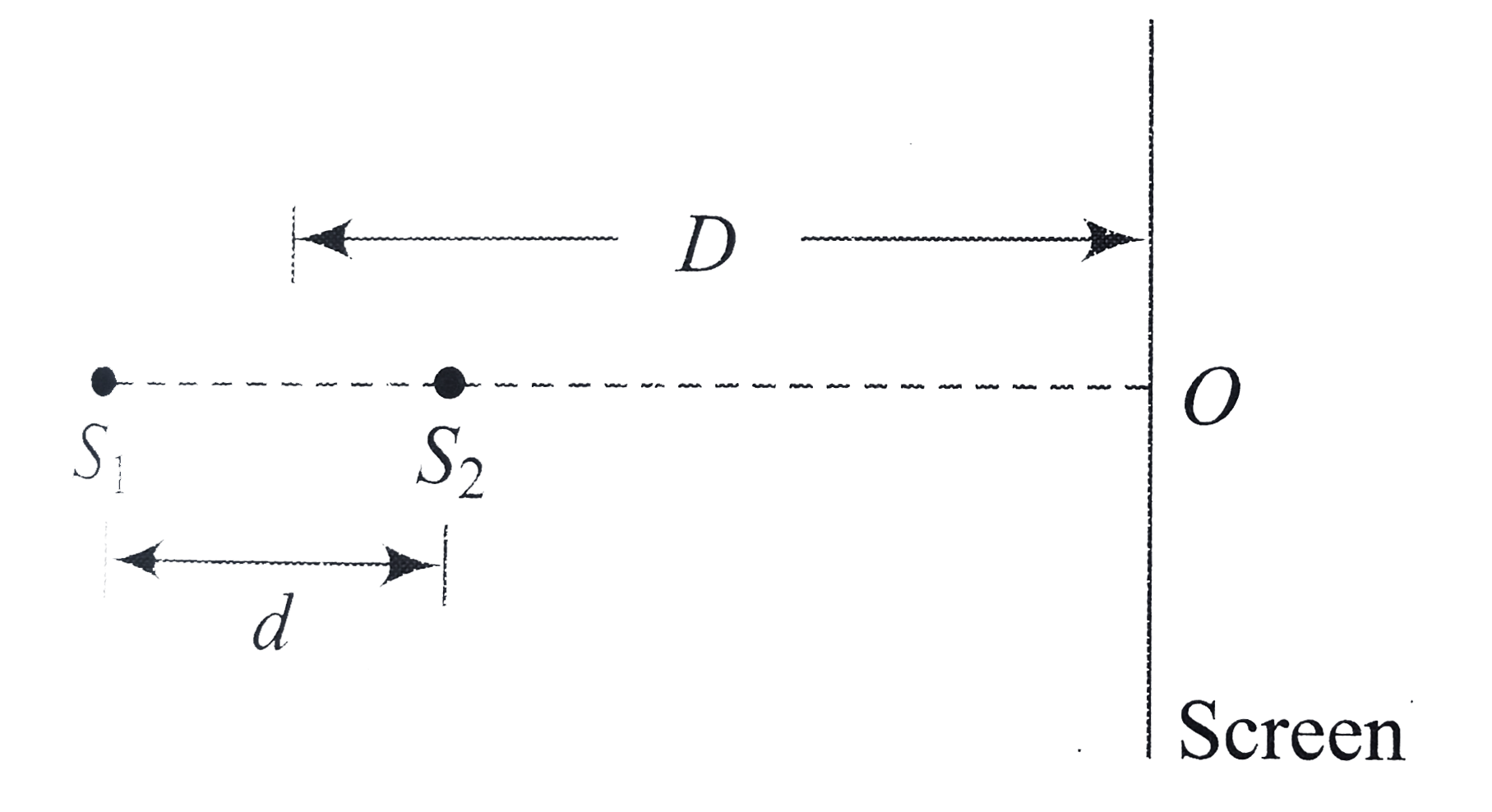 AIf d=7λ2,O will be minima.BIf d=λ, only one maxima can be observed on screen.CIf d=4.8λ then total 10 minimas would be there on screen.DIf d=5λ2, then intensity at O would be maximum.
AIf d=7λ2,O will be minima.BIf d=λ, only one maxima can be observed on screen.CIf d=4.8λ then total 10 minimas would be there on screen.DIf d=5λ2, then intensity at O would be maximum.
Why can’t two independent monochromatic sources of light emitting light of one and the same wavelength behave as coherent sources?
View SolutionTwo coherent sources emit light of wavelength λ. Separation between them, d=4λ.
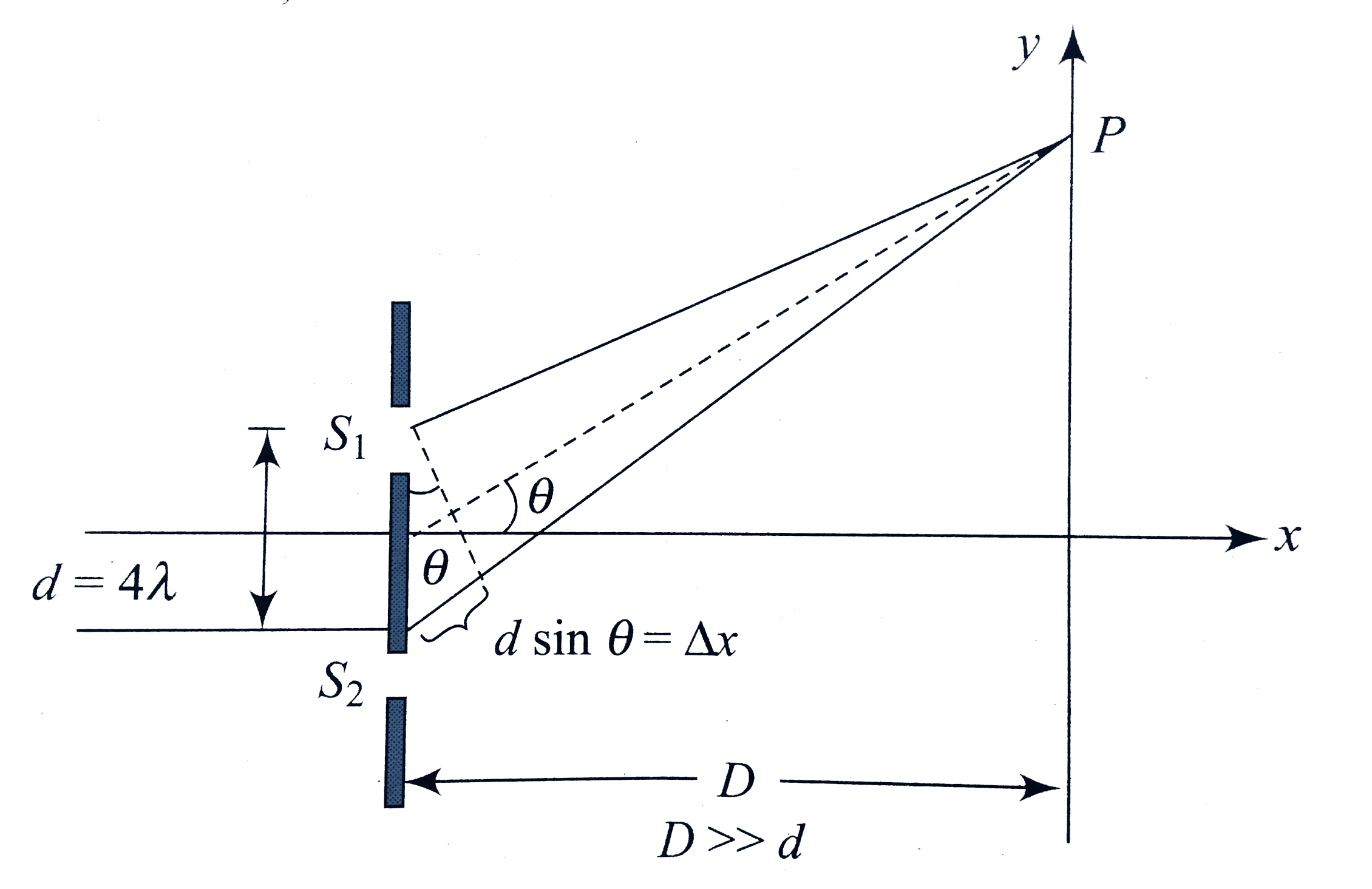
If a detector moves along the y-axis, what is the maximum number of minima observed?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is

View SolutionTwo identical coherent sources of wavelength λ are placed at (100λ,0) and (−50λ,0) along x-axis. The number of maxima and minima detected are ,respectively [include origin and (5λ,0)]
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
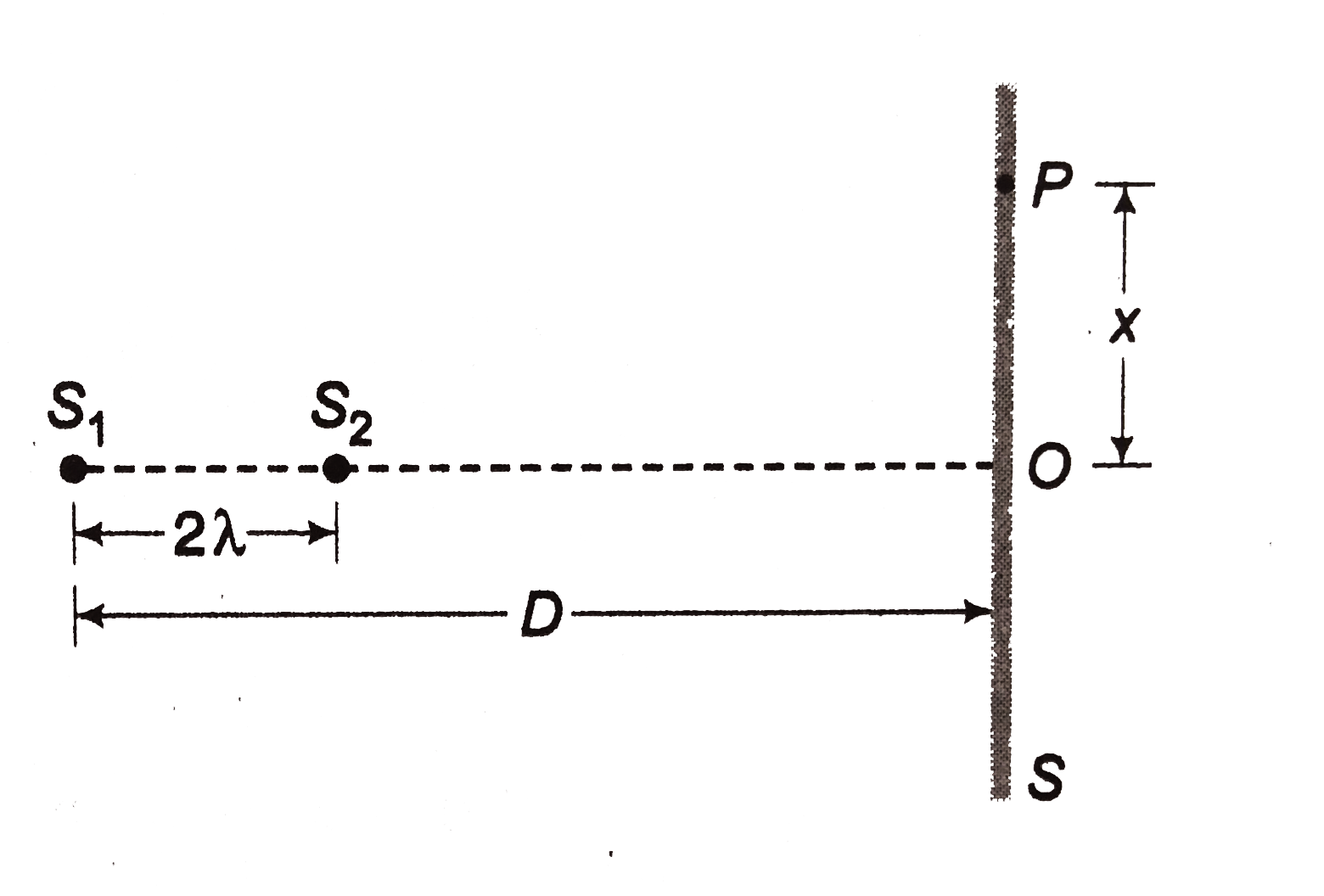 .
.
View SolutionThe figure shows two points source which emit light of wavelength λ in phase with each other and are at a distance d=5.5λ apart along a line which is perpendicular to a large screen at a distance L from the centre of the source. Assume that d is much less than L. Which of the following statement is (are) correct ?
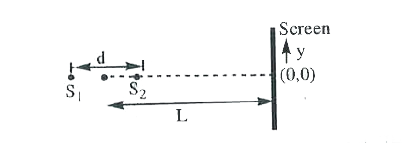
View Solution
