Two positively charged particles fixed in place on an x axis. The charges are q1=1.60×10−19Candq2=3.20×10−19C, and the particle separation is R = 0.0200m. What are teh magnitude and direction of the electrostatic force →F12 on particle 1 from particle 2?
To find the magnitude and direction of the electrostatic force →F12 on particle 1 from particle 2, we can use Coulomb's Law. The formula for the electrostatic force between two point charges is given by:
F=14πϵ0|q1q2|R2
where:
- F is the magnitude of the force between the charges,
- q1 and q2 are the magnitudes of the charges,
- R is the separation between the charges,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
1. Identify the given values:
- Charge q1=1.60×10−19C
- Charge q2=3.20×10−19C
- Separation R=0.0200m
2. Substitute the values into Coulomb's Law:
F=14πϵ0|q1q2|R2
3. Calculate the constant 14πϵ0:
14πϵ0≈9×109N m2/C2
4. Substitute the values of the charges and the separation:
F=9×109⋅(1.60×10−19)(3.20×10−19)(0.0200)2
5. Calculate (0.0200)2:
(0.0200)2=0.0004m2
6. Calculate the product of the charges:
(1.60×10−19)(3.20×10−19)=5.12×10−38C2
7. Substitute these values into the force equation:
F=9×109⋅5.12×10−380.0004
8. Calculate the force:
F=9×109⋅1.28×10−34=1.15×10−24N
9. Determine the direction of the force:
- Since both charges are positive, the force between them is repulsive. Therefore, the direction of the force on particle 1 due to particle 2 is away from particle 2.
Final Answer:
- Magnitude of the force: 1.15×10−24N
- Direction of the force: Repulsive, towards the negative x-direction (away from particle 2).
- F is the magnitude of the force between the charges,
- q1 and q2 are the magnitudes of the charges,
- R is the separation between the charges,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
- Charge q1=1.60×10−19C
- Charge q2=3.20×10−19C
- Separation R=0.0200m
F=14πϵ0|q1q2|R2
14πϵ0≈9×109N m2/C2
F=9×109⋅(1.60×10−19)(3.20×10−19)(0.0200)2
(0.0200)2=0.0004m2
(1.60×10−19)(3.20×10−19)=5.12×10−38C2
F=9×109⋅5.12×10−380.0004
F=9×109⋅1.28×10−34=1.15×10−24N
- Since both charges are positive, the force between them is repulsive. Therefore, the direction of the force on particle 1 due to particle 2 is away from particle 2.
- Magnitude of the force: 1.15×10−24N
- Direction of the force: Repulsive, towards the negative x-direction (away from particle 2).
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points9videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems63videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELASTICITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type1videos
ELECTRIC POTENTIAL
Similar Questions
Two point charges q1=2×10−3C and q2=−3×10−6C are separated by a distance x=10 cm. Find the magnitude and nature of the force between the two charges.
View SolutionIn Fig., the three particles are fixed in place and have charges q1=q2=+5e and q3=+2e. Distance a=3.00μm. What are the (a) magnitude and (b) direction of the net electric field at point P due to the particles ?
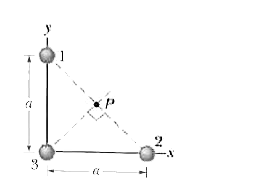 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If point charges Q1=2×10−7C and Q2=3×10−7C are at 30 cm separation, then find electrostatic force between them
A2×10−3NB6×10−3NC5×10−3ND1×10−3N
The charges and coordinates of two charged particles held fixed in an xy plane are q1=+3.0μC,x1=3.5cm,y1=0.50cm, and q2=−4.0μC,x2=−2.0cm,y2=1.5cm. Find the (a) magnitude and (b) direction of the electrostatic force on particle 1 due to particle 2. At what (c ) x and (d) y coordinates should a third particle of charge q3=+6.0μC be placed such that the net electrostatic force on particle 1 due to particles 2 and 3 is zero ?
View SolutionFigure 22-8c is identical to Fig. 22-8a except that particle 3 now lies on the x axis between particles 1 and 2. Particle 3 has charge q2=−3.20×10−19C and is at a distance (3/4)R from particle 1. What is the net electrostatic force →F1.net on particle 1 due to particles 2 and 3?
View SolutionIn Fig. , the particles have charges q1=−q2=300nC and q3=−q4=200nC, and distance a = 5.0 cm. What are the (a) magnitude and (b) angle (relative to the +x direction) of the net force on particle 3 ?
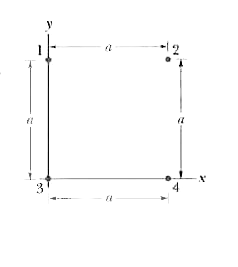 View Solution
View SolutionFigure shows two charged particles on an x axis : −q=−3.20×10−19C at x=−3.00m and q=3.20×10−19C at = + 3.00 m. What are (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the net electric field produced at point P at y = 4.00 m? (c ) What is the magnitude of the net field if y is doubled ?
 View Solution
View SolutionTwo point charges, q1=10×10−8Candq2=−2×10−8C, are separated by a distance of 60 cm in air.
Also calculate the electrostatic potential energy of the system.View SolutionIn fig. a central particle of charge −q is surrounded by two circular rings of charged particle of radii r and R, with Rgtr. what is the magnitude and dirction of the net electrostatic force on the central particle due to the other particles?
 View Solution
View SolutionTwo charged particles are placed at a distance 1.0 cm apart. What is the minimum possible magnitude of the electric force acting o each charge?
View Solution

