Two charged particles are placed at a distance 1.0 cm apart. What is the minimum possible magnitude of the electric force acting o each charge?
To find the minimum possible magnitude of the electric force acting on each charge when two charged particles are placed at a distance of 1.0 cm apart, we can use Coulomb's law. Here’s a step-by-step solution:
Step 1: Understand Coulomb's Law
Coulomb's law states that the electric force F between two point charges q1 and q2 separated by a distance r is given by the formula:
F=k|q1q2|r2
where:
- F is the electric force,
- k is Coulomb's constant (9×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
Step 2: Identify the Minimum Charge
The minimum possible charge is the elementary charge, which is the charge of an electron:
q=1.6×10−19C
Step 3: Substitute Values into the Formula
Given that the distance r=1.0cm=0.01m, we can substitute q1=q2=1.6×10−19C and r=0.01m into Coulomb's law:
F=k|q1q2|r2=9×109(1.6×10−19)(1.6×10−19)(0.01)2
Step 4: Calculate the Force
Now we can calculate the force:
F=9×109(1.6×10−19)2(0.01)2
Calculating (1.6×10−19)2:
(1.6×10−19)2=2.56×10−38
Now substituting this back into the equation:
F=9×1092.56×10−380.0001
F=9×109×2.56×10−34=2.304×10−24N
Conclusion
The minimum possible magnitude of the electric force acting on each charge is:
F≈2.3×10−24N
Coulomb's law states that the electric force F between two point charges q1 and q2 separated by a distance r is given by the formula:
F=k|q1q2|r2
where:
- F is the electric force,
- k is Coulomb's constant (9×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
The minimum possible charge is the elementary charge, which is the charge of an electron:
q=1.6×10−19C
Given that the distance r=1.0cm=0.01m, we can substitute q1=q2=1.6×10−19C and r=0.01m into Coulomb's law:
F=k|q1q2|r2=9×109(1.6×10−19)(1.6×10−19)(0.01)2
Now we can calculate the force:
F=9×109(1.6×10−19)2(0.01)2
Calculating (1.6×10−19)2:
(1.6×10−19)2=2.56×10−38
Now substituting this back into the equation:
F=9×1092.56×10−380.0001
F=9×109×2.56×10−34=2.304×10−24N
The minimum possible magnitude of the electric force acting on each charge is:
F≈2.3×10−24N
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
8 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
Two charged particles are placed at a distance r from each other. The magnitude of the electric force between the two charged particles is F. What will be the effect on F on placing the given charged particles in water? (Take dielectric constant of water 80).
View SolutionTwelve charges have been placed at the centre of each side of a cube as shown in the figure. Find the magnitude of Electric force acting on a charge Q placed at the centre of the cube. Take the side length of the cube to be r.
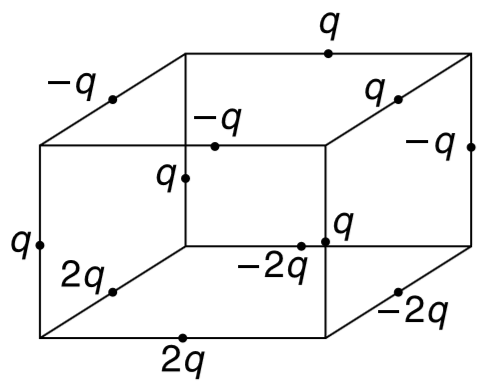
View Solution
Knowledge Check
Two charges are placed at a distance apart. It a glass slab is placed between them, force between them will
AincreaseBdecreaseCremain sameDbe zeroTwo charges are placed at certain distance apart. A metallic sheet is placed between them. What will happen to the force between the charges?
AIncreasesBDecreasesCRemains the sameDMay increase or decrease depending upon the shape of the metallic sheetTwo charges are placed at a distance apart if a glas slab is placed between them force between them will
Abe zeroBincreaseCdecreaseDremains the same
Two equal charges are placed at a separtion of 1.0 m. What should be the magnitude of the charges so that the force between them equals of a 50 kg person?
View SolutionTwo point charges q and −q are separated by the distance l, both being located at a distance l/2 from the infinite conducting plane. Find :
(a) the modulus of the electric force acting on each charge,
(b) the magnitude of the electric field strength vector at the midpoint between these charges.
View Solution" If two charges are placed at a distance of "5cm" .If a brass sheet is placed between them.The force between two charges will "
View Solution.If two charges are placed at a distance of "5cm" .If a brass sheet is placed between them.The force between two charges will
View SolutionTwo positively charged particles each having charge Q and are d distance apart. A third charge is introduced in midway on the line joining the two charges. Find the nature and magnitude of third charge so that the system is in equilibrium.
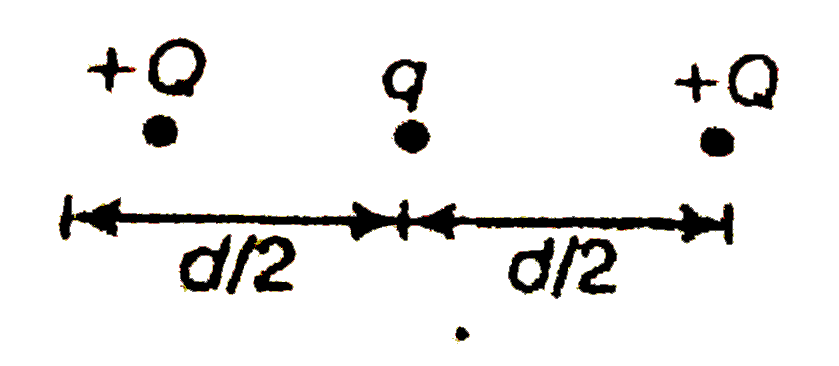
View Solution
