Two resistances of 100 ohm and 200 ohm are connected in series with a battery of emf 4 volt and negligible internal resistance. A voltmeter of resistance 200 ohm is used to measure voltage across the two resistances separately. Calculate the voltage indicated.
To solve the problem step by step, we will analyze the circuit with the given resistances and the voltmeter.
Step 1: Understand the circuit configuration
We have two resistances, R1=100Ω and R2=200Ω, connected in series with a battery of emf V=4V. The voltmeter, which has a resistance of Rv=200Ω, will be used to measure the voltage across each resistor separately.
Hint: Draw the circuit diagram to visualize the connections and components.
Step 2: Calculate the total resistance in the circuit
The total resistance Rt in the series circuit can be calculated as:
Rt=R1+R2=100Ω+200Ω=300Ω
Hint: Remember that in a series circuit, the total resistance is the sum of individual resistances.
Step 3: Calculate the total current in the circuit
Using Ohm's law, the total current I flowing through the circuit can be calculated as:
I=VRt=4V300Ω=175A≈0.01333A
Hint: Use Ohm's law V=IR to find the current.
Step 4: Calculate the voltage across each resistor without the voltmeter
The voltage across R1 (100 ohm) is:
V1=I⋅R1=(175A)⋅100Ω=10075V≈1.33V
The voltage across R2 (200 ohm) is:
V2=I⋅R2=(175A)⋅200Ω=20075V≈2.67V
Hint: The voltage drop across a resistor in a series circuit can be calculated by multiplying the current by the resistance.
Step 5: Calculate the effective resistance of the voltmeter when measuring
When the voltmeter is connected across R1, the effective resistance R1,eff is given by:
R1,eff=Rv⋅R1Rv+R1=200⋅100200+100=20000300≈66.67Ω
Hint: Use the formula for resistors in parallel to find the effective resistance.
Step 6: Calculate the new current with the voltmeter connected
The new total resistance when the voltmeter is connected across R1 is:
Rt,new=R1,eff+R2=66.67Ω+200Ω≈266.67Ω
The new current Inew is:
Inew=VRt,new=4V266.67Ω≈0.015A
Hint: The total resistance changes when additional components are added to the circuit.
Step 7: Calculate the voltage across R1 with the voltmeter connected
Now, the voltage across R1 with the voltmeter connected is:
V1,new=Inew⋅R1=0.015A⋅100Ω=1.5V
Hint: Use the new current to find the voltage across the resistor.
Step 8: Calculate the voltage across R2 with the voltmeter connected
The voltage across R2 can be calculated as:
V2,new=V−V1,new=4V−1.5V=2.5V
Hint: The total voltage in the circuit remains constant; use this to find the remaining voltage.
Final Answer
The voltmeter will indicate approximately:
- Across R1: 1.5V
- Across R2: 2.5V
We have two resistances, R1=100Ω and R2=200Ω, connected in series with a battery of emf V=4V. The voltmeter, which has a resistance of Rv=200Ω, will be used to measure the voltage across each resistor separately.
The total resistance Rt in the series circuit can be calculated as:
Rt=R1+R2=100Ω+200Ω=300Ω
Using Ohm's law, the total current I flowing through the circuit can be calculated as:
I=VRt=4V300Ω=175A≈0.01333A
The voltage across R1 (100 ohm) is:
V1=I⋅R1=(175A)⋅100Ω=10075V≈1.33V
V2=I⋅R2=(175A)⋅200Ω=20075V≈2.67V
When the voltmeter is connected across R1, the effective resistance R1,eff is given by:
R1,eff=Rv⋅R1Rv+R1=200⋅100200+100=20000300≈66.67Ω
The new total resistance when the voltmeter is connected across R1 is:
Rt,new=R1,eff+R2=66.67Ω+200Ω≈266.67Ω
Inew=VRt,new=4V266.67Ω≈0.015A
Now, the voltage across R1 with the voltmeter connected is:
V1,new=Inew⋅R1=0.015A⋅100Ω=1.5V
The voltage across R2 can be calculated as:
V2,new=V−V1,new=4V−1.5V=2.5V
The voltmeter will indicate approximately:
- Across R1: 1.5V
- Across R2: 2.5V
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA142videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
Two resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
View SolutionFigure below shows two resistors R1andR2 connected to a battery having an emf of 40 V and negligible internal resistance. A voltmeter having a resistance of 300 Ω is used to measure potential difference across R1 Find the reading of the voltmeter.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three resistances 2Ω,4Ω,5Ω are combined in series and this combination is connected to a battery of 12 V emf and negligible internal resistance. The potential drop across these resistances are
A(5,45,4.36,2.18)VB(2,18,5.45,4.36)VC(4.36,2.18,5.45)VD(2.18,4.36,5.45)V - Question 2 - Select One
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
Resistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View SolutionFour equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .
View SolutionA voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find the ratio of R1 and R2.
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionIn the circuit shows in Fig. 6.42, resistors X and Y, each with resistance R, are connected to a 6V battery of negligible internal resistance. A voltmeter, also of resistance R, is connected across Y.
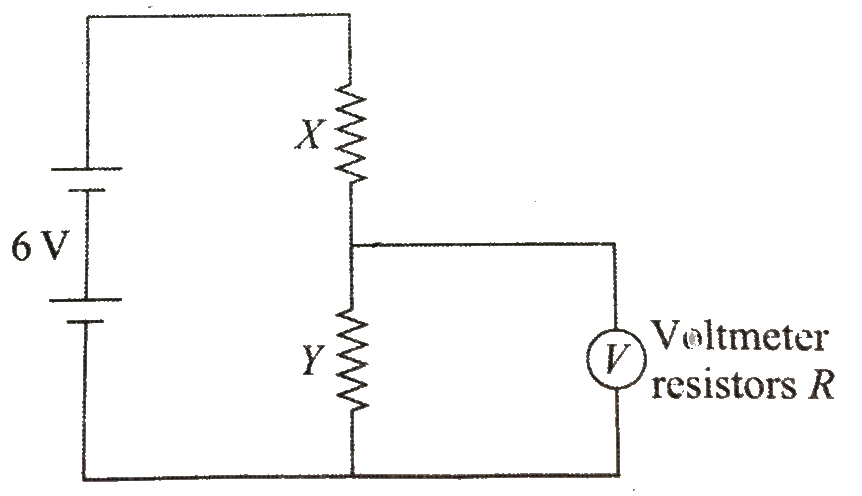
What is the reading of the voltmeter?View SolutionWhen two resistors of (600±3) ohm and (300±6) ohm are connected in parallel, value of the equivalent resistance is
View Solution

