Two resistors are connected (a) in series (b) in parallel The equivalent resistance in the two cases are $9 o h m$ and $2 o h m$ respectively. Then the resistances of the component resistor are

A

$2 o h m$ and $7 o h m$

B

$3 o h m$ and $6 o h m$

C

$3 o h m$ and $9 o h m$

D

$5 o h m$ and $4 o h m$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To solve the problem of finding the resistances of two resistors connected in series and parallel, we can follow these steps:
Step 1: Set Up the Equations
Let the two resistors be $R_{1}$ and $R_{2}$ .
1. When connected in series, the equivalent resistance $R_{s}$ is given by:
$R_{s} = R_{1} + R_{2}$
According to the problem, $R_{s} = 9 Ω$ . Therefore, we have:
$R_{1} + R_{2} = 9 (Equation 1)$
2. When connected in parallel, the equivalent resistance $R_{p}$ is given by:
$R_{p} = \frac{R_{1} \cdot R_{2}}{R_{1} + R_{2}}$
According to the problem, $R_{p} = 2 Ω$ . Therefore, we have:
$\frac{R_{1} \cdot R_{2}}{R_{1} + R_{2}} = 2 (Equation 2)$
Step 2: Substitute Equation 1 into Equation 2
From Equation 1, we can express $R_{1} \cdot R_{2}$ :
$R_{1} \cdot R_{2} = R_{p} \cdot (R_{1} + R_{2})$
Substituting $R_{p} = 2$ and $R_{1} + R_{2} = 9$ :
$R_{1} \cdot R_{2} = 2 \cdot 9 = 18 (Equation 3)$
Step 3: Solve the System of Equations
Now we have two equations:
1. $R_{1} + R_{2} = 9$ (Equation 1)
2. $R_{1} \cdot R_{2} = 18$ (Equation 3)
We can express $R_{1}$ in terms of $R_{2}$ using Equation 1:
$R_{1} = 9 - R_{2}$
Substituting this into Equation 3:
$(9 - R_{2}) \cdot R_{2} = 18$
Expanding this gives:
$9 R_{2} - R_{2}^{2} = 18$
Rearranging leads to:
$R_{2}^{2} - 9 R_{2} + 18 = 0$
Step 4: Solve the Quadratic Equation
We can solve the quadratic equation $R_{2}^{2} - 9 R_{2} + 18 = 0$ using the quadratic formula:
$R_{2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
Where $a = 1, b = - 9, c = 18$ :
$R_{2} = \frac{9 \pm \sqrt{(- 9)^{2} - 4 \cdot 1 \cdot 18}}{2 \cdot 1}$
Calculating the discriminant:
$R_{2} = \frac{9 \pm \sqrt{81 - 72}}{2} = \frac{9 \pm \sqrt{9}}{2} = \frac{9 \pm 3}{2}$
Thus, we have:
$R_{2} = \frac{12}{2} = 6 or R_{2} = \frac{6}{2} = 3$
Step 5: Find $R_{1}$
Using $R_{1} + R_{2} = 9$ :
1. If $R_{2} = 6$ , then $R_{1} = 9 - 6 = 3$ .
2. If $R_{2} = 3$ , then $R_{1} = 9 - 3 = 6$ .
Conclusion
The resistances of the two resistors are $R_{1} = 3 Ω$ and $R_{2} = 6 Ω$ (or vice versa).

|

Updated on:7/8/2024

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two resistors are connected (a) in series (b) in parallel. The equivalent resistance in the two cases are 9 ohm and respectively. Then the resistances of the component resistors are
A2 ohm and 7 ohm
B3 ohm and 6 ohm
C3 ohm and 9 ohm
D5 ohm and 4 ohm
Question 2 - Select One
Five resistors are connected as shown in the diagram. The equivalent resistance between $A$ and $B$ is

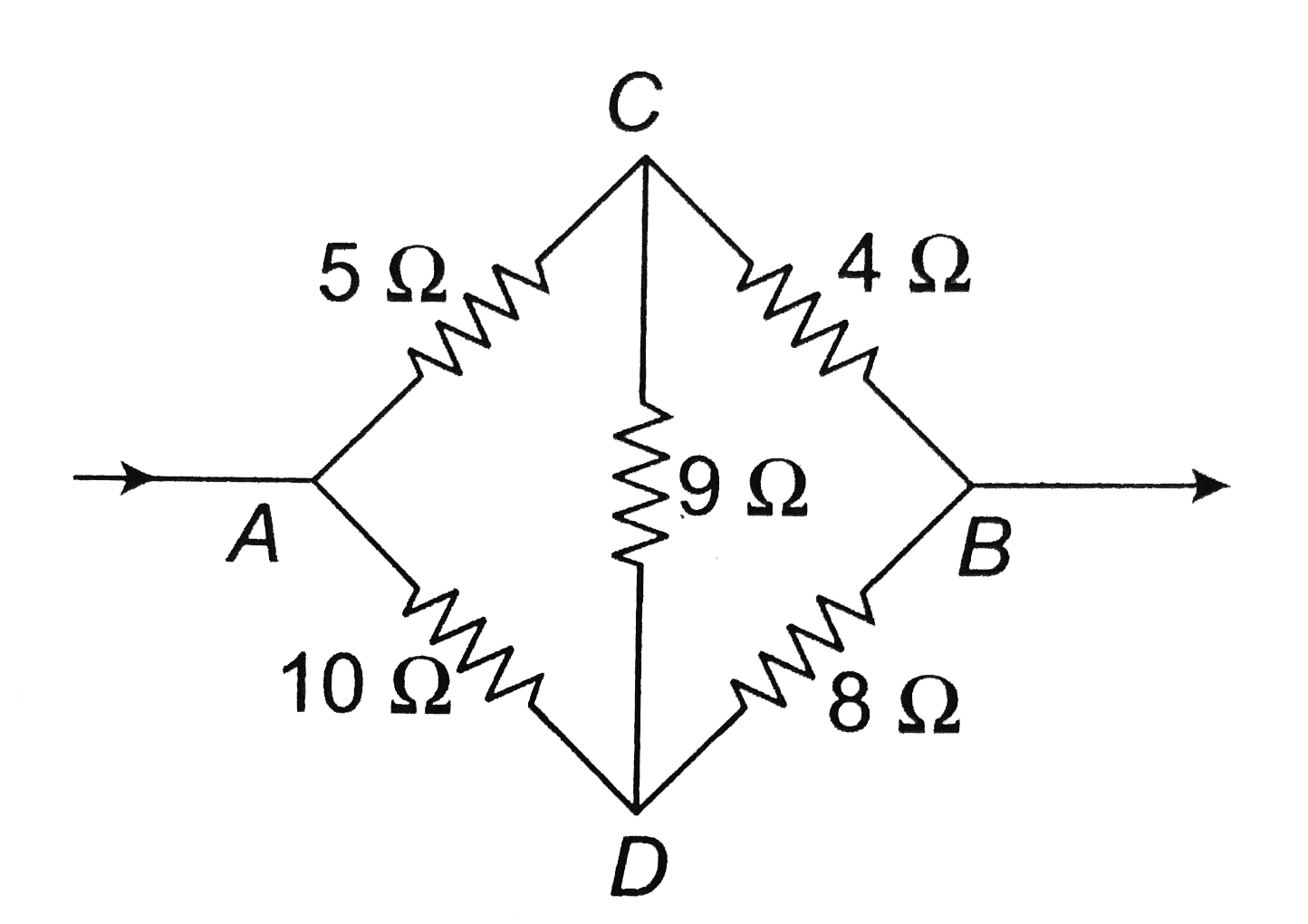A $6 o h m$
B $9 o h m$
C $12 o h m$
D $15 o h m$
Question 3 - Select One
A number of resistors are connected as shown in the figure. The equivalent resistance between A and B is

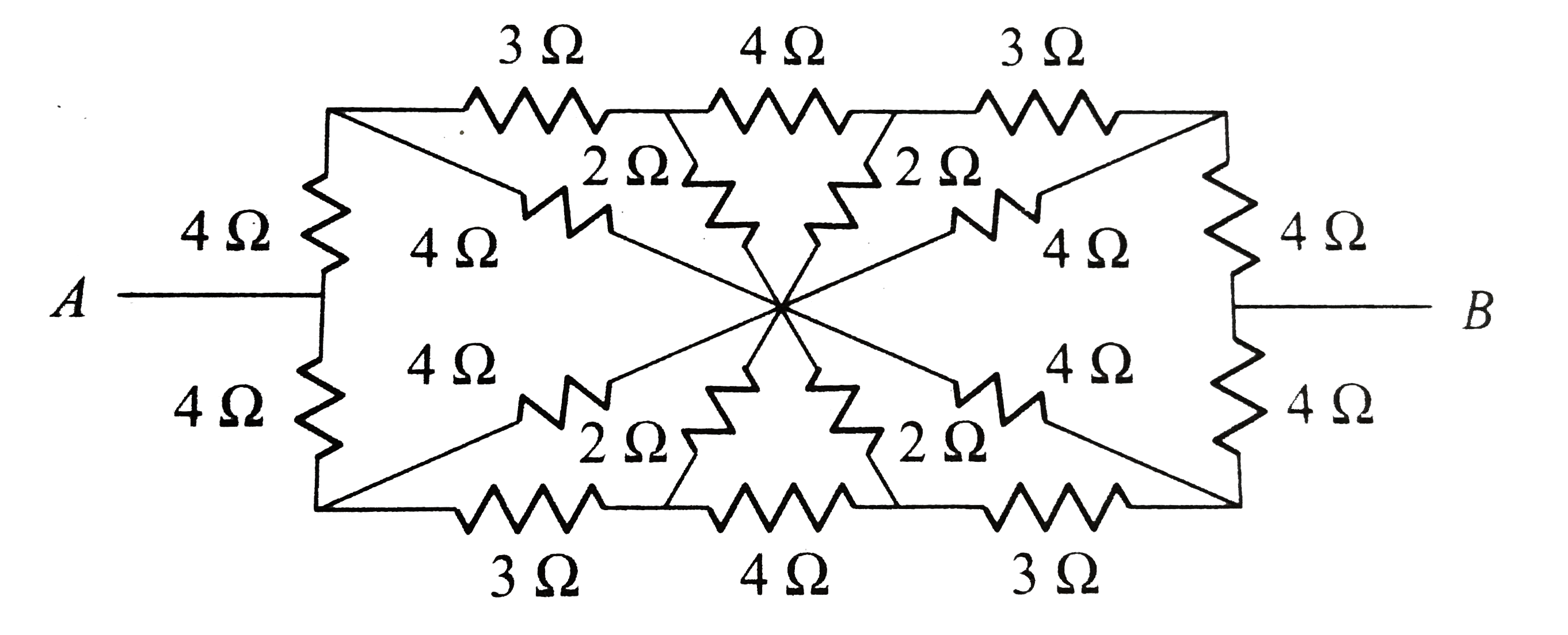A $6 Ω$
B $12 Ω$
C $9 Ω$
D $15 Ω$

A2Z-CURRENT ELECTRICITY-Combination And Resistivity

Home
Ask Doubt
Profile