Two ships A and B are 10km apart on a line running south to north. Ship A farther north is streaming west at 20km/h and ship B is streaming north at 20km/h. What is their distance of closest approach and how long do they take to reach it?
The correct Answer is:A, B
Ships A and B are moving with same speed 20km/h in the directions shown in figure. It is a two dimensional, two body problem with zero acceleration.
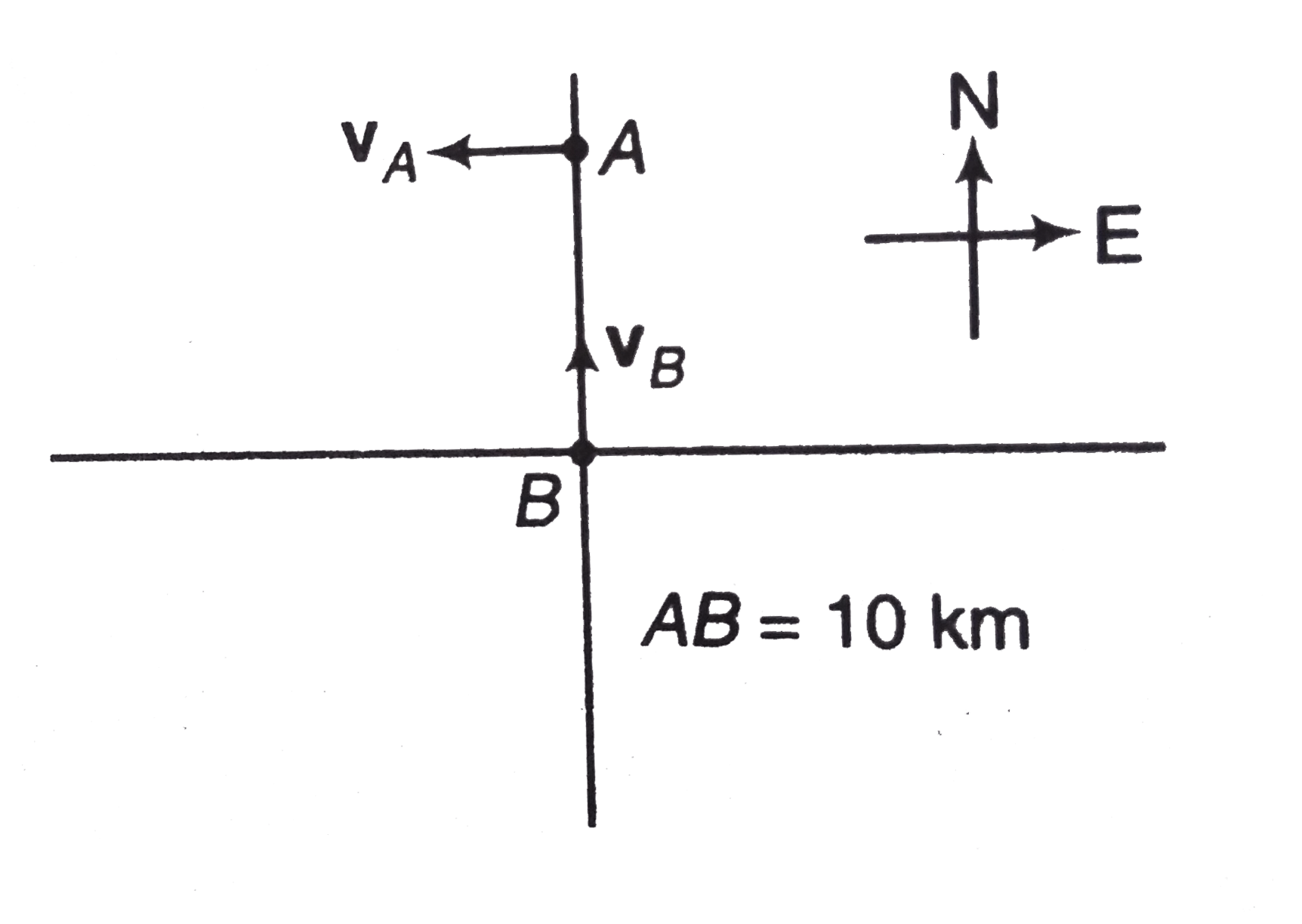
Let us find vBA.
∴VBA=vB−vA
Here, |vBA|=√(20)2+(20)2
=20√2km/h
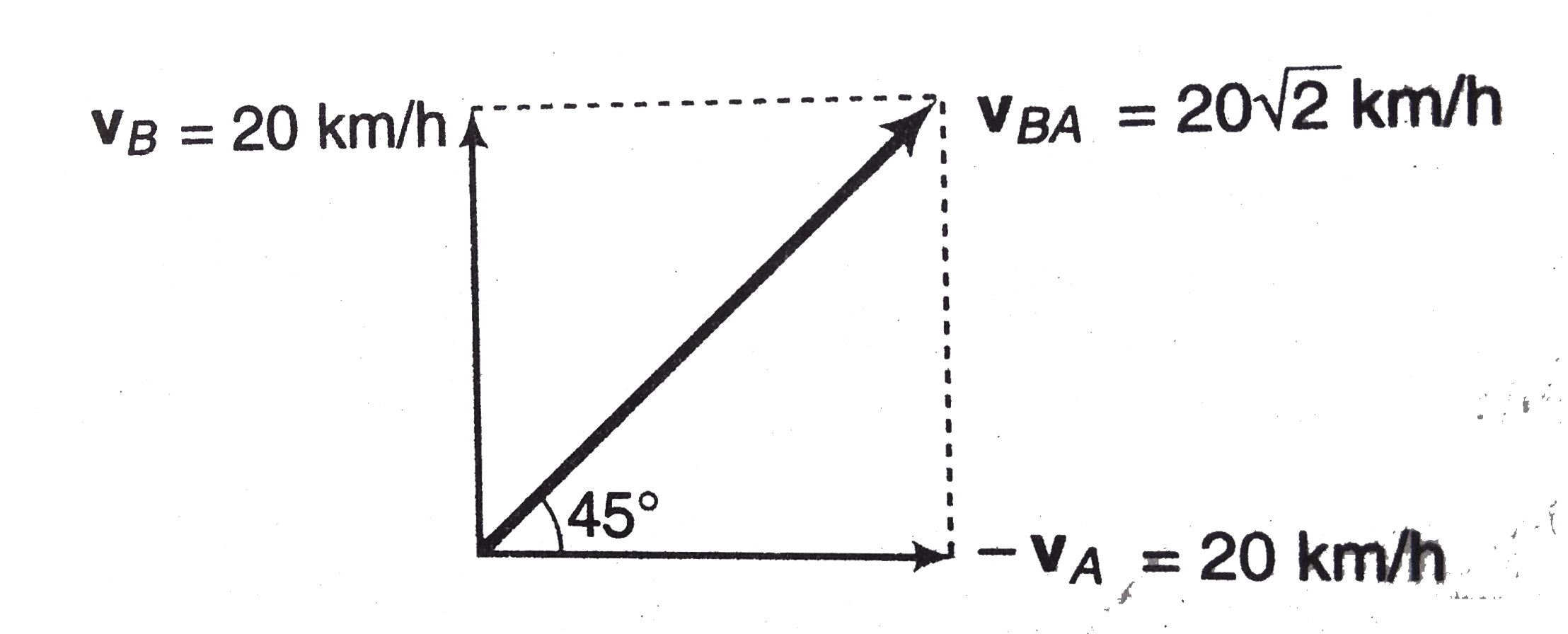
i.e. vBA is 20√2km/h at an angle of 45∘ from east towards north. Thus, the given problem can be
simplified as A is at rest and B is moving with vBA in the direction
shown in fig
Therefore, the minimum distance between the two is
smin=AC=ABsin45∘
=10(1√2)km
=5√2km
and the desired time is
t=BC|vBA|=5√220√2(BC=AC=5√2km)
=14h=15min

Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 1
1 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 2
1 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Two ships are 10km apart on a line joining south to north. The one farther north is steaming west at 20kmh−1. The other is steaming north at 20kmh−1. What their distance of closest approach ? How long do they take to reach itb ?
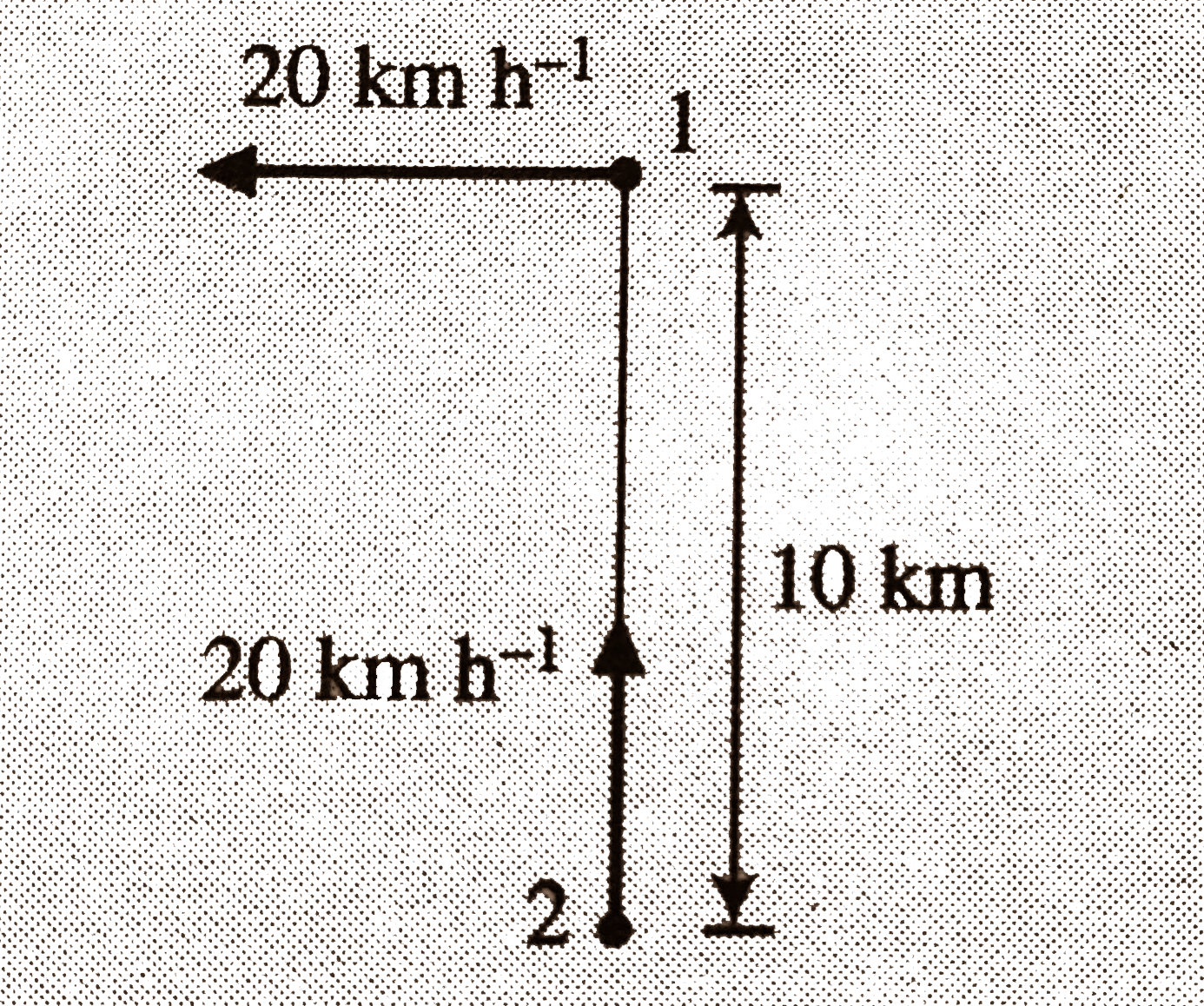 .
.
View SolutionTo ships 10 km apart on a line running south to north . The one father north is steaming west at 20 km/h. The other is steaming north at 20 km/h. The distance of closest approach is . . . . to reach it the time taken is . . . .
View Solution
Knowledge Check
Two ships are 10km apart on a line from south to north.The one farther north is moving towards west at 40kmph and the other is moving towards north at 40kmph.Then distance of their closest approach is
A10kmB10√2kmC10√2kmD20kmTwo ships are 10√2 km apart on a line running south to north. The one further north is moving west with a speed of 25 km/h, while the other towards north with a speed of 25 km/h.
ATheir distance of closest approach is 5√2 km.BTheir distance of closest approach is 10 kmCTime required to reach the closest distance is 17 minDTime required to reach the closest distance is 29 min.A car A going north-east at 80km/h and another car B is going south-east at 60km/h. The direction of the velocity of A relative to B makes an angle with the north equal to:
Atan−1(2/7)Btan−1(7/2)Ctan−1(7)Dtan−1(1/7)
Two boat A and B 20 km apart as shown. Boat a streaming east and boat B in north by 30km/hr then find shortest approach and time taken for it.

View SolutionAt a certain two cars area each 10km from the intersection of roads that are perpendiuclar. Cat A is moving east at 30 km/hr while car B moves north at 50km/hr both toward the intersection. (a) Fnd their closest distance of approach . (B) Where are A and B when they are closest?
View SolutionA person goes 10 km north and 20 km east. What will be the displacement from initial point?
View SolutionTwo trains A and B ,100km apart are travelling towards each other on different tracks with same starting speed of 50km/h. The train A accelerates at 20km/h2 and the train B retards at the rate 20km/h2. The distance covered by the train A when they cross each other is
View SolutionA person goes 10km north and 20km east. What will be displacement from initial point ?
View Solution
