Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle $θ$ that the threads will make with the vertical due to attraction between the balls is :

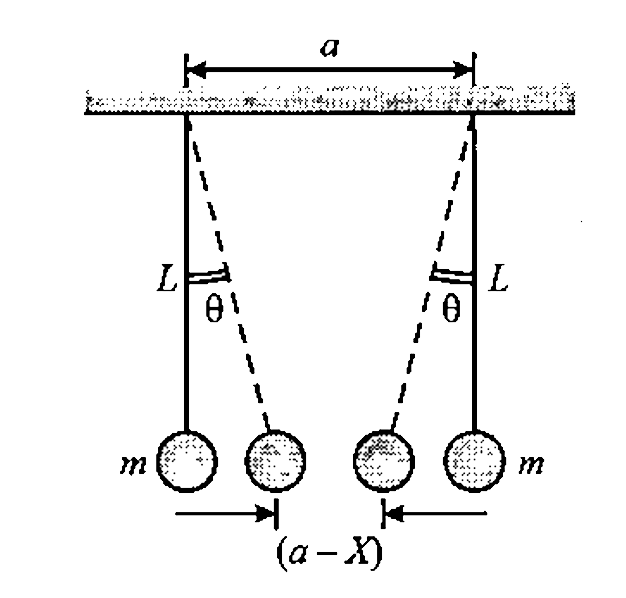
${tan}^{- 1} \frac{(a - X) g}{m G}$

${tan}^{- 1} \frac{m G}{{(a - X)}^{2} g}$

${tan}^{- 1} \frac{{(a - X)}^{2} g}{m G}$

${tan}^{- 1} \frac{(a^{2} - X^{2}) g}{m G}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle theta that the threads will make with the vertical due to attraction between the balls is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Two metallic balls of mass $m$ are suspended by two strings of length $L$ . The distance between upper ends is $l$ . The angle at which the string will be inclined with vertical due to attraction is $(m < < M$ where M is the mass of Earth)
A ${tan}^{- 1} (\frac{G m}{g l^{2}}$
B ${tan}^{- 1} (\frac{G m}{g L^{2}}$
C ${tan}^{- 1} (\frac{G m}{g l})$
D ${tan}^{- 1} (\frac{G m}{g L})$
Question 2 - Select One
Two spherical objects each of radii R and masses m1 and m2 are suspended using two strings of equal length L as shown in the figure $(R < < L)$ . The angle, $θ$ which mass $m_{2}$ makes with the vertical is approximately -

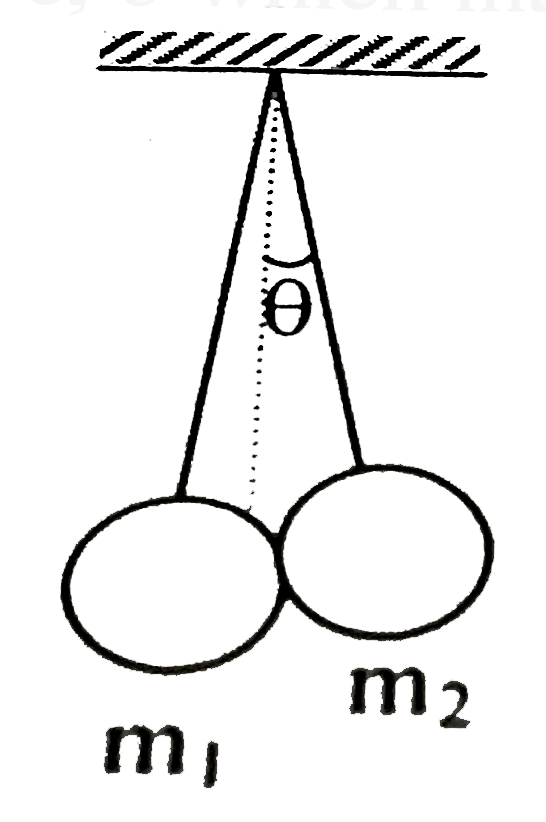A $\frac{m_{1} R}{(m_{1} + m_{2}) L}$
B $\frac{2 m_{1} R}{(m_{1} + m_{2}) L}$
C $\frac{2 m_{2} R}{(m_{1} + m_{2}) L}$
D $\frac{m_{2} R}{(m_{1} + m_{2}) L}$
Question 3 - Select One or More
A small sphere of mass $m$ suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of $θ$ measured from the vertical is $g \sqrt{1 + 3 {cos}^{3} θ}$
BThread tension as a function of $θ$ measured from the vertical is $T = 3 m g cos θ$
CThe angle $θ$ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is ${cos}^{- 1} 1 / \sqrt{3}$ .
DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be $m g$ .

PHYSICS GALAXY - ASHISH ARORA-GRAVITATION-Numerial MCQs

Home
Ask Doubt
Profile

Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two metallic balls of mass m are suspended by two strings of length L. The distance between upper ends is l. The angle at which the string will be inclined with vertical due to attraction is (m<<M where M is the mass of Earth)

Two spherical objects each of radii R and masses m1 and m2 are suspended using two strings of equal length L as shown in the figure (R<<L). The angle, θ which mass m2 makes with the vertical is approximately -

A small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then

PHYSICS GALAXY - ASHISH ARORA-GRAVITATION-Numerial MCQs

Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle $θ$ that the threads will make with the vertical due to attraction between the balls is :

Two metallic balls of mass $m$ are suspended by two strings of length $L$ . The distance between upper ends is $l$ . The angle at which the string will be inclined with vertical due to attraction is $(m < < M$ where M is the mass of Earth)

Two spherical objects each of radii R and masses m1 and m2 are suspended using two strings of equal length L as shown in the figure $(R < < L)$ . The angle, $θ$ which mass $m_{2}$ makes with the vertical is approximately -

A small sphere of mass $m$ suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then