Two small balls of the same size and of masses m1 and m2(m1>m2) are tied by a thin weightless thread and dropped from a balloon. The tension T of the thread during the flight towards the ground after the motion of the balls has become steady state is (steady state means that the balls are coming down with uniform velocity due to the forces weight, air friction and upthrust). Consider that air is still without any wind below, during the motion of the balls through air:
zero
(m1−m2)g2
(m1+m2)g2
m1g
The correct Answer is:B
2T=(m1−m2)g
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct15videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason4videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice30videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice35videos
BASIC MATHEMATICS
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
Similar Questions
Two small balls of the same size and of mass m1 and m2(m1>m2) are tied by a thin weightless thread and dropped from a ballon. Determine the tension T of the thread during the flight after the motion of the balls has become steady-state.
View SolutionTwo small balls of the same size and of mass m1 and m2(m1>m2) are tied by a thin weightless thread and dropped from a ballon. Determine the tension T of the thread during the flight after the motion of the balls has become steady-state.
View Solution
Knowledge Check
- Question 1 - Select One
Two balls of same size but different masses m1 and m2(m2>m1) are attached to the two ends of a thin light thread and dropped from a certain height. It is known that the ciscous drag of air depends on the size and velocities of the balls. other than the gravitational pull from the earth and the viscous drag, the buoyant force from air also act on the balls, the buoyant force on a ball equals to the wweight of air displaced by the ball. After sufficiently long time from the instant the balls were dropped both of them acquire uniform velocity known as terminal velocity. When the balls have acquired terminal velocity, the tension in the thread is
AzeroB(m2−m1)gC0.5(m2+m1)gD0.5(m2−m1)g - Question 2 - Select One
A ball is dropped from a balloon which is rising up with a speed of 2 m/s. After 2 s the velocity of the packet is
A20 m/sB18 m/sC22 m/sDnone
Two small balls of the same size and of mass m1 and m2(m1>m2) are tied by a thin light thread and dropped from a large height. Determine the tension T of the thread during the flight after the motion of the balls has become steady. (Air resistance force is same on two balls)
[Take m1=2kg, m2=1kg, g=10m/s2]View SolutionTwo small balls of the same size and of mass m1 and m2(m1>m2) are tied by a thin light thread and dropped from a large height. Determine the tension T of the thread during the flight after the motion of the balls has become steady. (Air resistance force is same on two balls)
[Take m1=2kg, m2=1kg, g=10m/s2]View SolutionTwo bodies with masses m1 and m2>m1 connected by a thread lie on a smooth table. A force Q is first applied to the larger and then to the smaller of the bodies (Fig.). Is the tension of the thread in both cases the same?
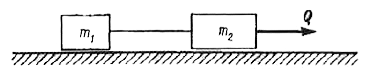 View Solution
View SolutionA ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
View SolutionA ball is dropped from a ballon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
View SolutionA ball is dropped from a balloon rising up with a velocity of 50 m/s. When the ball is dropped the balloon was at a height of 100 m. Find the time taken by the ball to reach the ground.
View Solution
