Two small kids weighing 10 kg and 15 kg respectively are trying to balance a seesaw of total length 5.0 with the fulcrum at the centre. If one of the kids is sitting at an end where should the other sit?
To solve the problem of balancing the seesaw with two kids of different weights, we will follow these steps:
Step 1: Understand the setup
- We have two kids: Kid A weighing 10 kg and Kid B weighing 15 kg.
- The seesaw is 5 meters long, with the fulcrum at the center, meaning each side of the seesaw is 2.5 meters long.
Step 2: Identify the positions
- Kid A (10 kg) is sitting at one end of the seesaw, which is 2.5 meters from the fulcrum.
- We need to find the position of Kid B (15 kg) such that the seesaw is balanced.
Step 3: Set up the torque equation
- The torque due to Kid A about the fulcrum is given by:
TorqueA=mA⋅g⋅dA
where mA=10kg, g is the acceleration due to gravity, and dA=2.5m.
- The torque due to Kid B about the fulcrum is:
TorqueB=mB⋅g⋅dB
where mB=15kg and dB is the distance from the fulcrum where Kid B is sitting.
Step 4: Apply the equilibrium condition
- For the seesaw to be balanced, the total torque on both sides must be equal. Therefore, we can write:
TorqueA=TorqueB
This gives us:
mA⋅g⋅dA=mB⋅g⋅dB
Step 5: Simplify the equation
- Since g appears on both sides, we can cancel it out:
mA⋅dA=mB⋅dB
Substituting the known values:
10⋅2.5=15⋅dB
Step 6: Solve for dB
- Now, we can solve for dB:
25=15⋅dB
dB=2515=53≈1.67m
Conclusion
- Kid B should sit approximately 1.67 meters from the fulcrum on the opposite side to balance the seesaw.
- We have two kids: Kid A weighing 10 kg and Kid B weighing 15 kg.
- The seesaw is 5 meters long, with the fulcrum at the center, meaning each side of the seesaw is 2.5 meters long.
- Kid A (10 kg) is sitting at one end of the seesaw, which is 2.5 meters from the fulcrum.
- We need to find the position of Kid B (15 kg) such that the seesaw is balanced.
- The torque due to Kid A about the fulcrum is given by:
TorqueA=mA⋅g⋅dA
where mA=10kg, g is the acceleration due to gravity, and dA=2.5m.
TorqueB=mB⋅g⋅dB
where mB=15kg and dB is the distance from the fulcrum where Kid B is sitting.
- For the seesaw to be balanced, the total torque on both sides must be equal. Therefore, we can write:
TorqueA=TorqueB
This gives us:
mA⋅g⋅dA=mB⋅g⋅dB
- Since g appears on both sides, we can cancel it out:
mA⋅dA=mB⋅dB
Substituting the known values:
10⋅2.5=15⋅dB
- Now, we can solve for dB:
25=15⋅dB
dB=2515=53≈1.67m
- Kid B should sit approximately 1.67 meters from the fulcrum on the opposite side to balance the seesaw.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
Two persons A and B of weight 80kg and 50kg respectively are standing at opposite ends of a boat of mass 70kg and length 2m at rest. When they interchange their positions then displacement of the centre of mass of the boat will be :-

View SolutionTwo particles of mass 5 kg and 10 kg respectively are attached to the twoends of a rigid rod of length 1 m with negligible mass. the centre of mass of the system from the 5 kg particle is nearly at a distance of :
View Solution
Knowledge Check
Two masses A and B of 10 kg and 5 kg respectively are connected with a string passing over a frictionless pulley fixed at the corner of a table as shown in Fig. 15.4.1. The co-efficient of friction of A with the table is 0.2 The minimum mass of C that may by placed on A to prevent it from moving is equal to
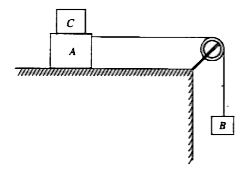 A1 5 kgB10 kgC4 kgD0 kg
A1 5 kgB10 kgC4 kgD0 kg
Two persons of masses 55kg and 65kg respectively are at the opposite ends of a boat. The length of the boat is 3.0m and weights 100kg. The 55kg man walks up to the 65kg man and sits with him. If the boat is in still water the centre of mass of the system shifts by.
View SolutionTwo perons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat. The length of the boat is 3 m and weight 100 kg. The 55 kg man walks upto the 65 kg man and with him. If the boat is in still water the centre of mass of the system shifts by
View SolutionTwo blocks of masses 2 kg and 1 kg respectively are tied to the ends of a string which passes over a light frictionless pulley . The masses are held at rest at the same horizontal level and then released . The distance traversed by centre of mass in 2 s is ( g = 10 m/s2)
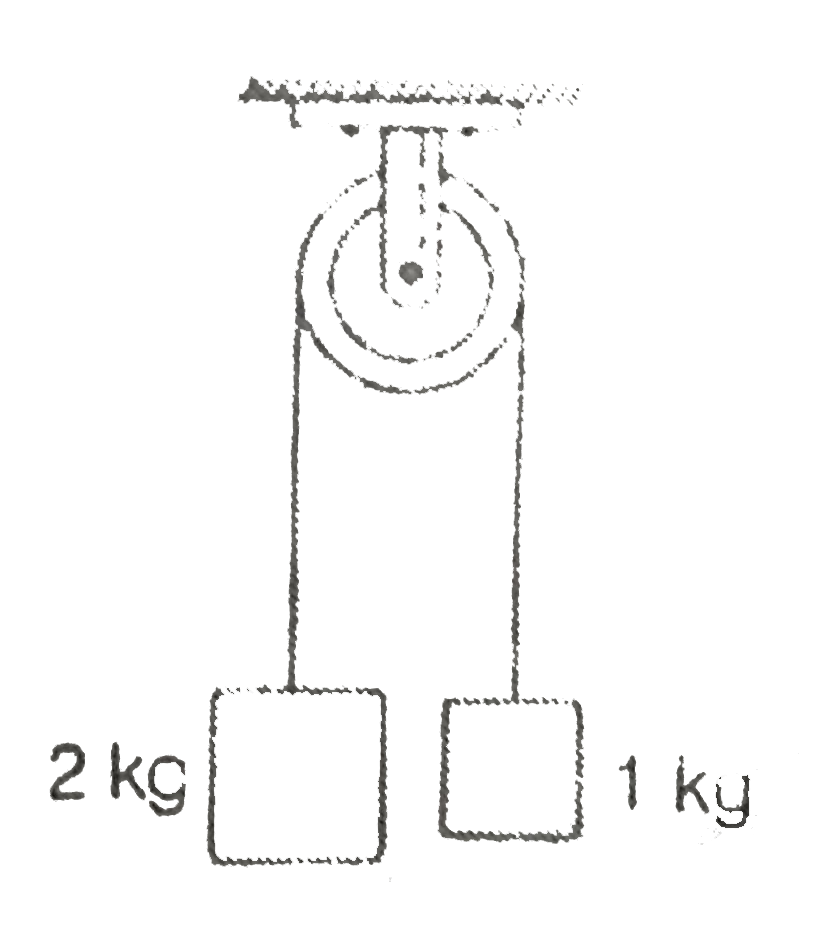
View SolutionTwo bodies of masses 0.5 kg and 1 kg are lying in the X-Y plane at points (-1, 2) and (3, 4) respectively. Locate the centre of mass of the system.
View SolutionTwo masses A and B of 10kg and 5kg, respectively , are connected with a string passing over a frictionless pulley fixed at the corner of a table as shown. The coefficient of static friction between A and the table is 0.2. The minimum mass C that should be placed on A to prevent it from moving is equal to

View SolutionTwo masses A and B of 10kg and 5kg, respectively , are connected with a string passing over a frictionless pulley fixed at the corner of a table as shown. The coefficient of static friction between A and the table is 0.2. The minimum mass C that should be placed on A to prevent it from moving is equal to

View SolutionTwo uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05kg, moving horizontally, hits the lower end of the combination and sticks to it what should be the velocity of the object so that the system could just be reised to the horizontal position.
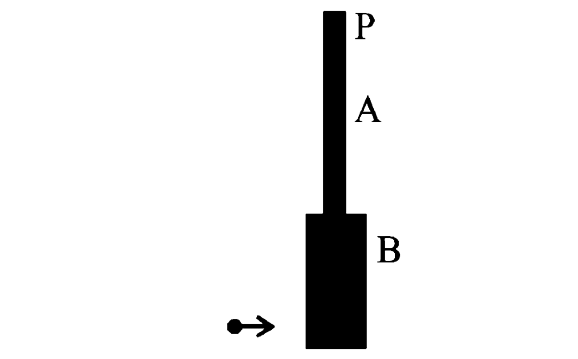
View Solution
