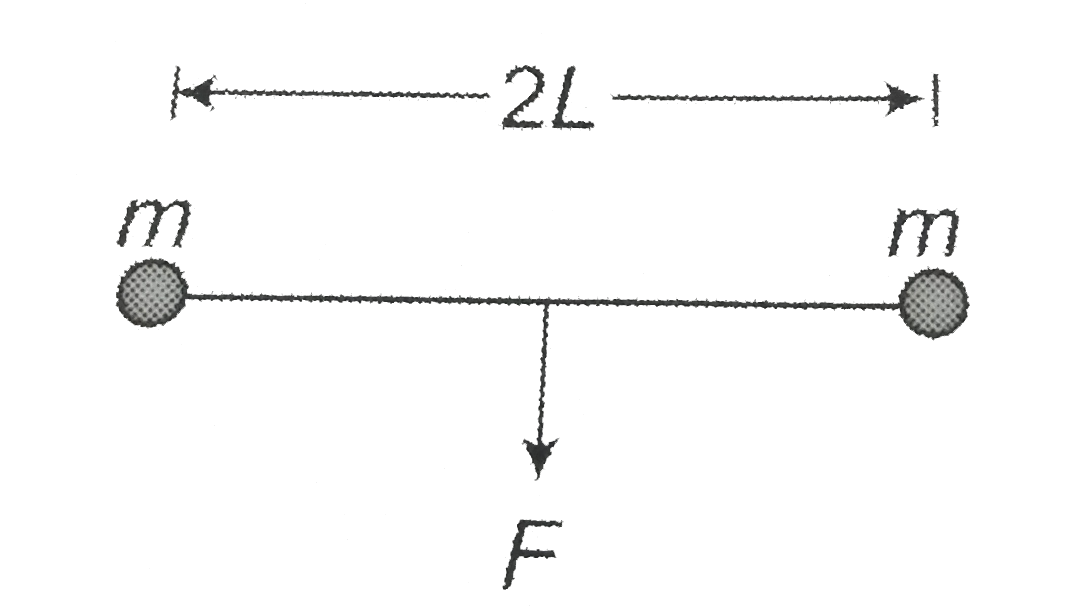
Two small sphere each of mass $m$ connected by a string of length 2l are kept on a smooth horizontal surface. A vertical force $F$ is applied at the middle of the string. What is maximum value of $F$ for which the sphere do not lose contact with the surface?

A

2mg

B

mg

C

$\frac{3 m g}{2}$

D

4mg

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$F = 2 T \sin θ$
$T \sin θ + N = m g$
$N = m g - T \sin θ$
For no contact:
$N > 0$
implies $m g - T \sin θ > 0$
implies $m g - \frac{F}{2} > 0$ implies $F < 2 m g$
So $F_{max} = 2 m g$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

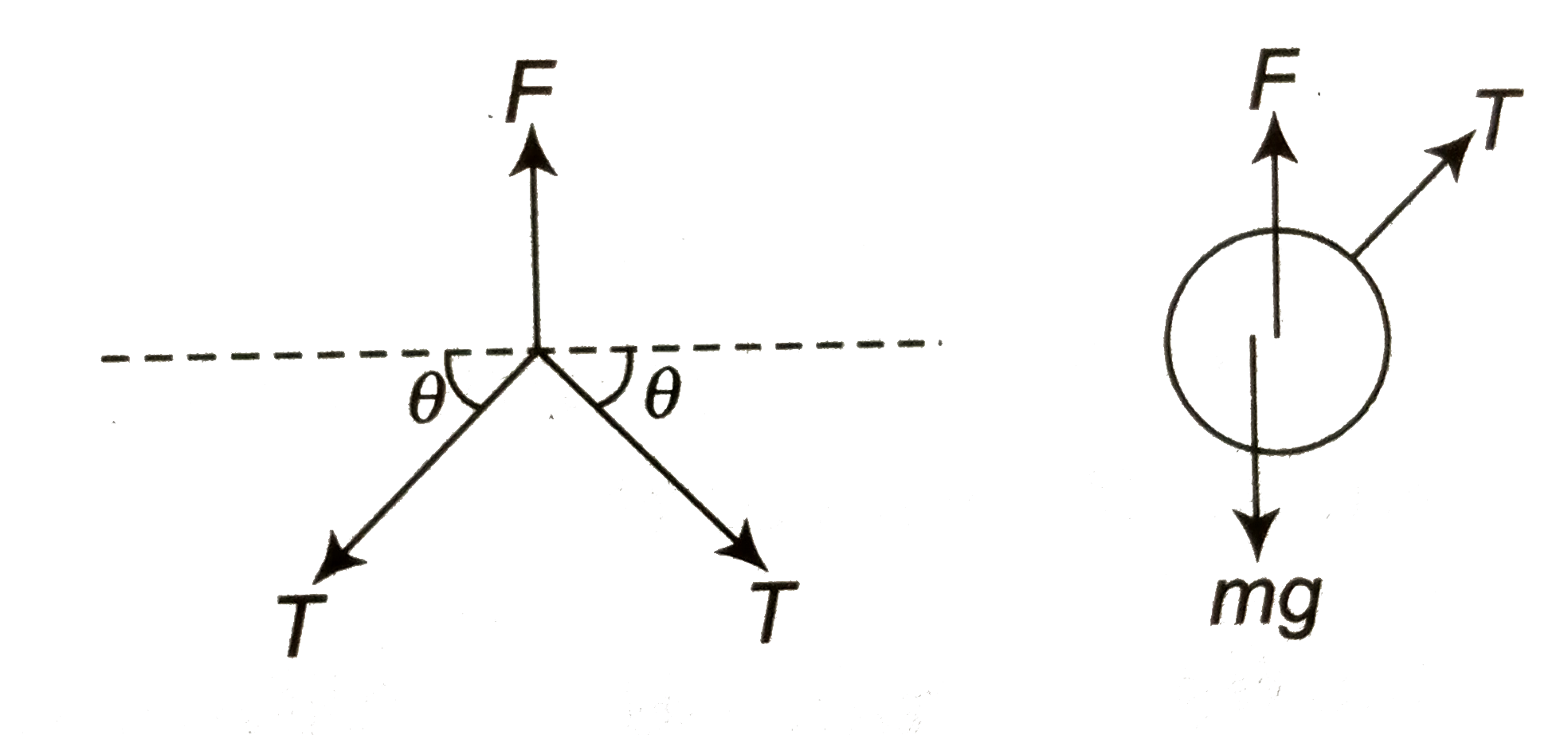
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Four blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.

A $T_{3} = \frac{1}{4} F$
B $T_{2} = \frac{1}{2} F$
C $T_{1} = \frac{3}{4} F$
D $T_{1} = T_{2} = T_{3} = \frac{1}{2} F$
Question 2 - Select One
A solid sphere of radius $R$ is placed on a smooth horizontal surface. A horizontal force $F$ is applied at height $h$ from the lowest point. For the maximum acceleration of the centre of mass
A $h = R$
B $h = 2 R$
C $h = 0$
Dthe acceleration will be same whatever $h$ may be
Question 3 - Select One
A hollow cylinder of mass m and radius r is kept on a smooth horizontal surface. Horizontal force F is applied at a height above the centre. Find the value of h/R so that ring performs pure rolling on the surface.
A1
B $\frac{1}{2}$
C $\frac{1}{3}$
D $\frac{2}{5}$

A2Z-NEWTONS LAWS OF MOTION-Applications Of Newton'S Laws Of Motion

Home
Ask Doubt
Profile