Two sources of current of equal emf are connected in series and having different internal resistance and . Find the external resistance at which the potential difference across the terminals of one of the sources becomes equal to zero.
and for both the sources are equal. Therefore, potential difference () will be zero for a source having greater internal resistance i.e.
or
or
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.16videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.21videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 61videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two cells of emf 2E and E with internal resistance r1 and r2 respectively are connected in series to an external resistor R (see figure). The value of R, at which the potential difference across the terminals of the first cell becomes zero is
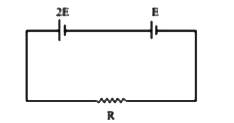 View Solution
View SolutionTwo cells of same emf ε but internal resistances r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
AV=E/(R+r)BV=ECV=E/(1+r/R)DV=E/(1+R/r) - Question 2 - Select One
Tow cells with the same emf E and different internal resistances r1 and r2 are connected in series to an external resistances R . The value of R so that the potential difference across the first cell be zero is
A√r1r2Br1+r2Cr1−r2Dr1+r22 - Question 3 - Select One
Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero.
Ar1−r2Br1+r22Cr1−r22Dr1+r2
According to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
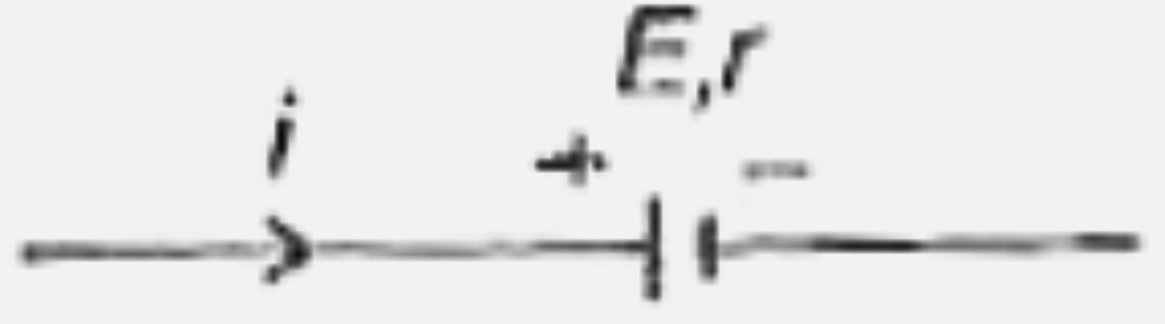 View Solution
View SolutionIn the given circuit, if the potential difference across the internal resistance r1 is equal to E, then the resistance R is equal to:
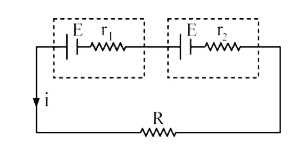 View Solution
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero.
View SolutionTwo sources of emf 6V and internal resistance 3Ω and 2Ω are connected to anexternal resistance R as shown. If potential difference across battery A is zero, then the value of R ( in Ω) is
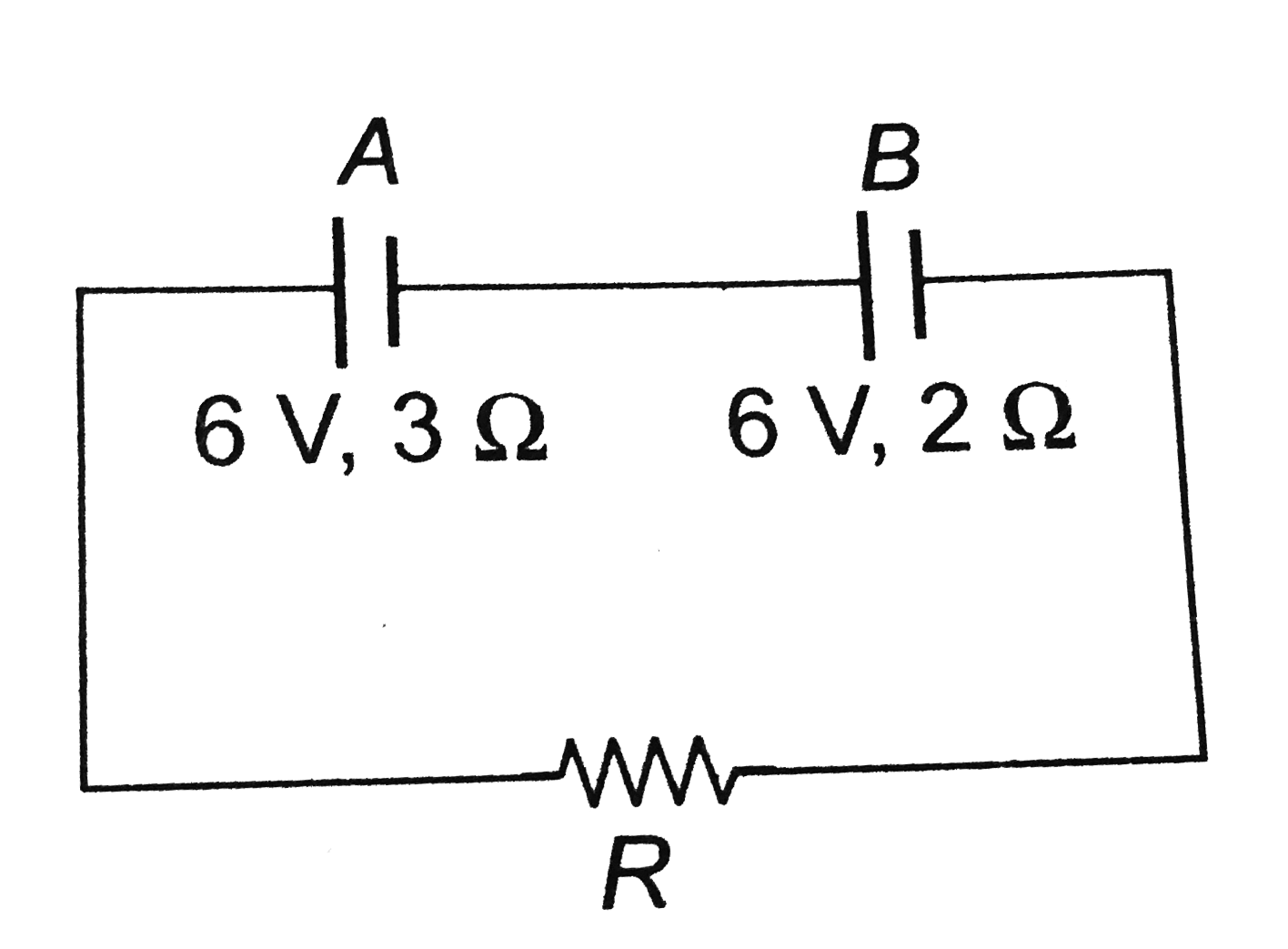 View Solution
View SolutionTwo sources of equal emf are connected to an external resistance R. The internal resistance of the two sources are R1andR2(R1>R1). if the potential difference across the source having internal resistance R2 is zero, then
View Solution

