Two cells of same emf ε but internal resistances r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.

Here net emf of combination = 2ε and net resistance of the circuit = r1+r2+R
Current flowing in the circuit I=2εr1+r2+R
As potential difference across first cell V1=ε−Ir1=0, hence
ε−2ε(r1+r2+R)r1=0 or ε[r1+r2+R−2r1]=0
⇒R=r1−R2
Topper's Solved these Questions
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS - II
8 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SELF ASSESSMENT TEST (SECTION A (MULTIPLE CHOICE QUESTIONS))
6 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS
42 Videos
- CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION D
6 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
3 Videos
Similar Questions
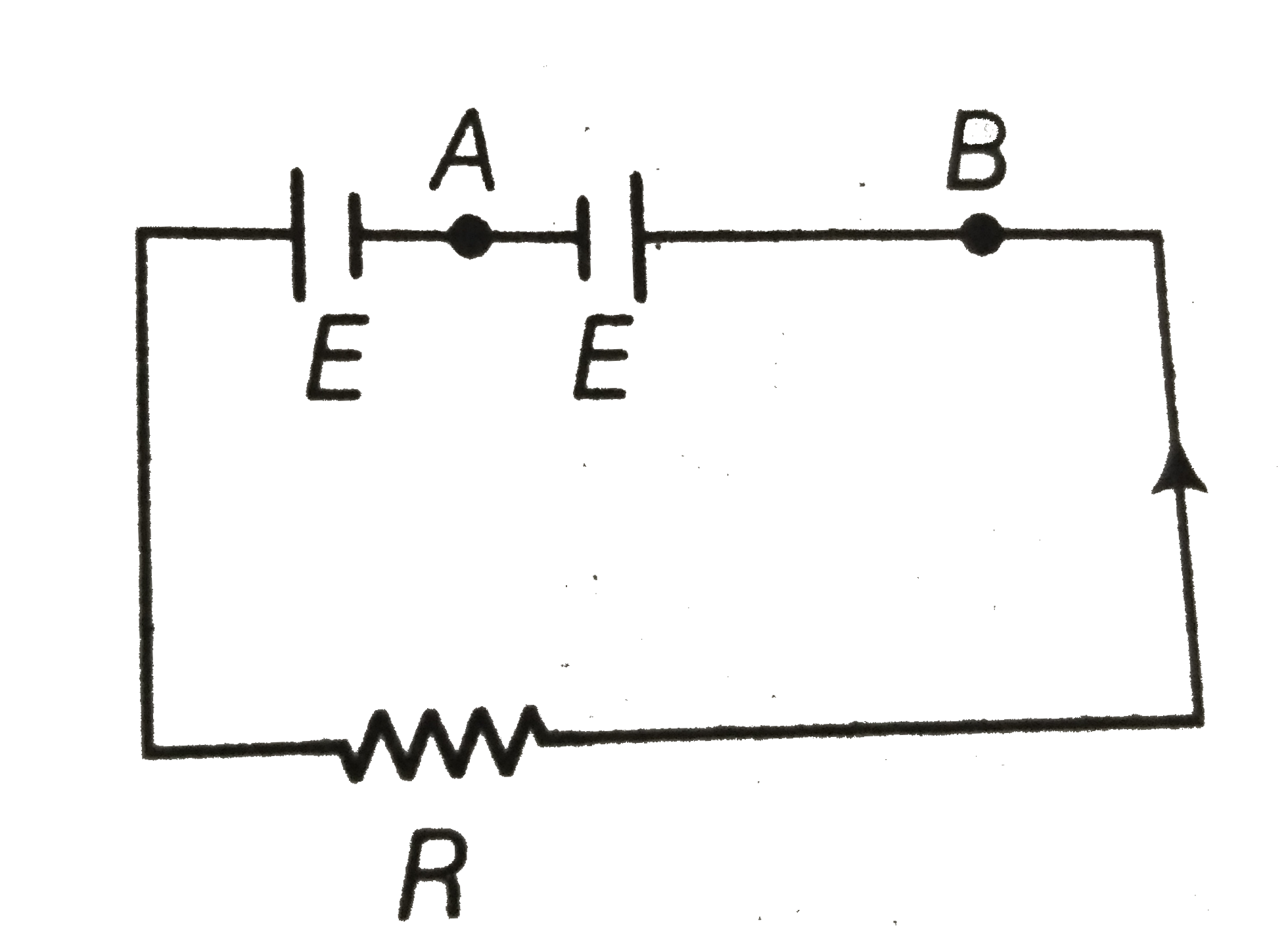
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
View Solution
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
View Solution
Knowledge Check
Tow cells with the same emf E and different internal resistances r1 and r2 are connected in series to an external resistances R . The value of R so that the potential difference across the first cell be zero is
A√r1r2Br1+r2Cr1−r2Dr1+r22Two cell with the same e.m.f. E and difference internal resistance r1andr2 are connected in series to an external resistance R a value of R be selected such that the potential difference as the flow cell E should be zero when
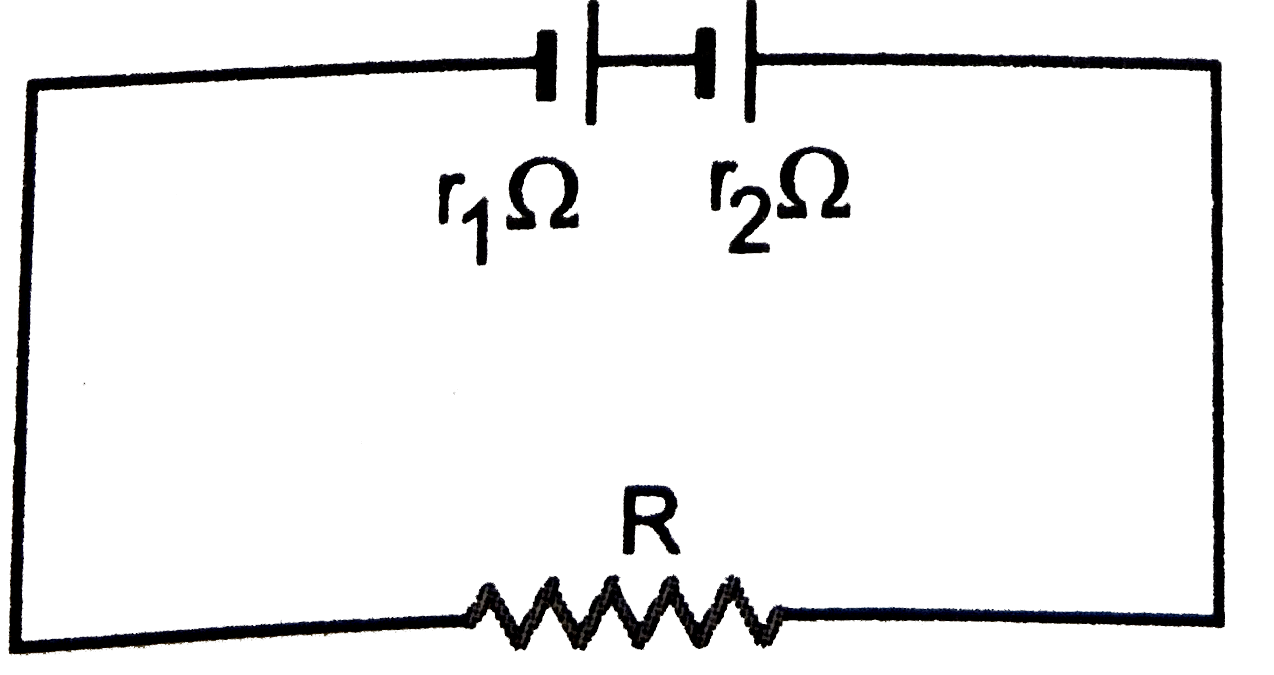 AR=r1+r2BR=r1−r2CR=r1/r2DR=r1=r2
AR=r1+r2BR=r1−r2CR=r1/r2DR=r1=r2Two cells of same emf ε but of different internal resistances r1 and r2 are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
Ar1+r2Br1−r2Cr2−r1Dr21/r2
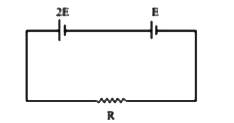
Two cells of emf 2E and E with internal resistance r1 and r2 respectively are connected in series to an external resistor R (see figure). The value of R, at which the potential difference across the terminals of the first cell becomes zero is
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View Solution
