Two stars each of mass M and radius R are approaching each other for a head-on collision. They start approaching each other when their separation is r>>R. If their speed at this separation are negligible, the speed v with which they collide would be
v=√GM(1R−1r)
v=√GM(12R−1r)
v=√GM(1R+1r)
v=√GM(12R+1r)
The correct Answer is:B
(b) Since the speeds of the stars are negligible when they are at a distance r, hence the initial kinetic energy of the system is zero. Therefore, the initial total energy of the systme is
Ei=KE+PE=0+(−GMMr)=−GM2r
where M represent the mass of each star and r is initial seperation between them.
When two stars collide their centres will be at a distance twice the radius of a star i.e. 2R.
Let v be the speed with which two stars collide. Then total energy of the system at the instant of their collision is given by.
Ei=KE+PE=0+(−GMMr)=−GM2r
where M represents the mass of each star and r is initial separation between them.
When two stars collide their centres will be at a distancee twice the radius of a star i.e., 2R
Let v be the speed with which two stars collide. Then total energy of the system at the instant of their collision is given by
Ef=2×(12Mv2)+(−GMM2R)=Mv2−GM22R
According to law of conservation of mechanical energy
Ef=Ei
Mv2−GM22R=−GM2rorv2=GM(12R−1r)orv=√GM(12R−1r)
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Geostationary And Polar Satellites
7 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Weightlessness
2 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Earth Satellite
4 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Two starts each of one solar mass (=2×1030kg) are approaching each other for a head on collision. When they are a distance 109km. their speeds are negligible. What is the speed with which they collide? The radius of each star is 104km. Assume the stars to remain undistorted until they collide. (Use the known value of G).
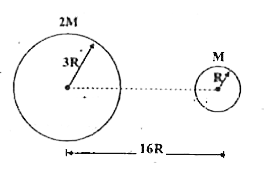
View SolutionTwo spherical bodies of masses 2M and M and radii 3R and R respectively are held at a distance 16R from each other in free space. When they are released they start approaching each other due to the gravitational force of attraction , then find
(a) the ratio of their accelerations during their motion
(b) their velocitites at the time of impact.
View Solution
Knowledge Check
Two particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
Am1m2vBZeroC(m1−m2)vm1+m2Dm2m1vTwo pulses on a string approach each other at speeds of 1m/s what is the shape of the string at t=6s?
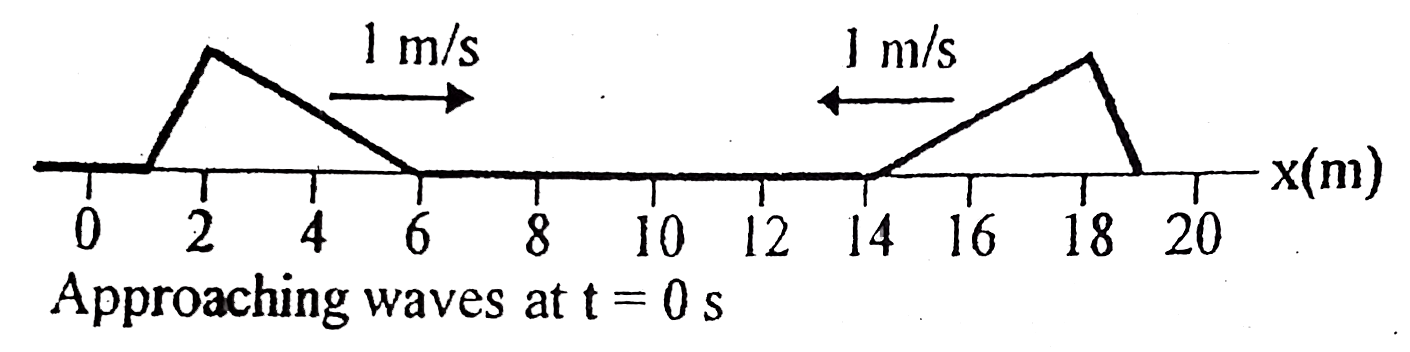 A
A B
B C
C D
D
Two particles of mass m and M are initially at rest and infinitely separated from each other. Due to mutual interaction, they approach each other.
Their relative velocity of approach at a separation d between them, isA[2 GdM + m]1/2B[2 G(M+m)d]1/2C2 GM+mdDNone of these
Two spheres of masses 2M and M are initially at rest at a distance R apart. Due to mutual force of attraction, they approach each other. When they are at separation R/2, the acceleration of the centre of mass of spheres would be
View SolutionWhat will happen when two clouds with unlike charges approach each other?
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
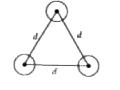
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
View Solution
