Two steel rods and an aluminium rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 00C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αaandαs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
steel
Aluminium
Steel

Let the initial length of the system at 0∘C
=l0
When temperature changes by θ
Final length of the steel at system temperature.
So, strain of the system=l−(l0)l0
Steel
Aluminium
Steel
But the total strain of the system
= total stress of system/ total Young's modulus of system
Now, total stress due to two steel rod
+ stress due to aluminium
=(γsαsθ)+(γsαsθ)+((γAl)(αAl)θ)
=(2γsαsθ)+(γAlαAlθ)
Now Young's modulus system
=γs+γs+γAl=(2γs+γAl
∴Stra∈ofsystem=(2γsαsθ)+γAlαAlθ2γs+γAl
l−ll0=(2γsαsθ)+(γAlαAlθ)2γs+γAl
l= (l_0)[ 1+((2gamma_s alpha_s theta)+(2gamma_(Al) alpha_(Al) theta) / (2 gamma_s+ gamma_(Al))
Topper's Solved these Questions
Similar Questions
Two steel rods and an aluminum rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminum and steel are αaandαs respectively. Young's modulus of aluminum is Ya and of steel is Ys.

View SolutionTwo Aluminium rods and a steel rod of equal cross-sectional area and equal length l0 are joined rigidly side by side as shown in figure. Initially the rods are at 0∘C. Find the length of the rod at the temperature θ if young's modulus of elasticity of the aluminium and steel are Ya and Ys respectively and coefficient of linear expansion of aluminum and steel are αa and αs respectively.
∣∣ ∣∣AluminiumSteelAluminium∣∣ ∣∣
View Solution
Knowledge Check
A steel rod of length L0 . has a cross sectional area A. The force required to stretch this rod by the same amount as the expansion produced by heating it through ΔT is (coefficient of linear expansion of steel is α and young's modulus for steel is Y ).
AYAαΔTB1/2YAαΔTC2YAαΔTD3YAαΔTA thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
AL0[1+α(θ1+θ2)]BL0(1+α(θ1+θ22))CL0(1+αθ1)DL0(1+α(θ1+θ22))
An iron rod of length 50 cm is joined at an end to aluminium rod of length 100 cm. All measurements refer to 20_0 C . Find the length of the composite system at 1000 C. and its average coefficent of linear expansion. The coefficient o f linear expansion o f iron and aluminium are 10 xx 10_-6 0 C_-1 and 24 xx10_-6 0 C _-1 respectively.
View SolutionTwo same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
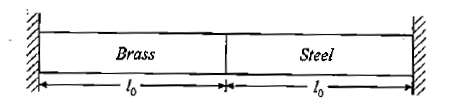
View SolutionWhat should be the sum of lengths of an aluminium and steel rod at 0∘C is, so that all the temperature their difference in length is 0.25m. (Take coefficient of linear expansion for aluminium and steel at 0∘C as 22×10−6/.∘C and 11×10−5/.∘C respectively.)
View SolutionWhat should be the sum of lengths of an aluminium and steel rod at 0∘C is, so that all the temperature their difference in length is 0.25m. (Take coefficient of linear expansion for aluminium and steel at 0∘C as 22×10−6/.∘C and 11×10−5/.∘C respectively.)
View SolutionA thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
View SolutionFind the ratio of the lengths of an iron rod and an aluminium rod for which the difference in the lengths in independent of temperature. Coefficients of linear expansion of iron and aluminium are 12×10−60C^(−1)and23×10−60C(−1)respectively.
View Solution
