Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and −q. The potential difference between the centres of the two rings is
(a) q2π∈0[1R−1√R2−d2]
(b) qR4π∈0d2
(c) q4π∈0[1R−1√R2+d2]
(d) zero
The correct Answer is:A
To find the potential difference between the centers of two thin wire rings with charges +q and -q, we can follow these steps:
Step 1: Understand the Setup
We have two rings:
- Ring A with charge +q
- Ring B with charge -q
The distance between the centers of the rings is d, and both rings have a radius R.
Step 2: Calculate the Potential at the Center of Ring A (Va)
The potential at the center of Ring A due to its own charge +q is given by the formula:
Va=14πϵ0⋅qR
where ϵ0 is the permittivity of free space.
Step 3: Calculate the Potential at the Center of Ring A Due to Ring B
The potential at the center of Ring A due to Ring B (which has charge -q) is calculated considering the distance from the center of Ring B to the center of Ring A, which is √R2+d2:
VA due to B=14πϵ0⋅−q√R2+d2
Step 4: Total Potential at the Center of Ring A (Va)
The total potential at the center of Ring A is the sum of the potentials due to its own charge and the charge of Ring B:
Va=14πϵ0⋅qR−14πϵ0⋅q√R2+d2
Va=q4πϵ0(1R−1√R2+d2)
Step 5: Calculate the Potential at the Center of Ring B (Vb)
Using similar logic, the potential at the center of Ring B due to its own charge -q is:
Vb=14πϵ0⋅−qR
And the potential at the center of Ring B due to Ring A (which has charge +q) is:
VB due to A=14πϵ0⋅q√R2+d2
Step 6: Total Potential at the Center of Ring B (Vb)
The total potential at the center of Ring B is:
Vb=−q4πϵ0R+q4πϵ0√R2+d2
Vb=q4πϵ0(1√R2+d2−1R)
Step 7: Calculate the Potential Difference (ΔV)
The potential difference between the centers of the two rings is:
ΔV=Va−Vb
Substituting the expressions for Va and Vb:
ΔV=q4πϵ0(1R−1√R2+d2)−q4πϵ0(1√R2+d2−1R)
Step 8: Simplify the Expression
Combining the two terms gives:
ΔV=q4πϵ0(2R−2√R2+d2)
ΔV=q2πϵ0(1R−1√R2+d2)
Final Result
Thus, the potential difference between the centers of the two rings is:
ΔV=q2πϵ0(1R−1√R2+d2)
We have two rings:
- Ring A with charge +q
- Ring B with charge -q
The distance between the centers of the rings is d, and both rings have a radius R.
The potential at the center of Ring A due to its own charge +q is given by the formula:
Va=14πϵ0⋅qR
where ϵ0 is the permittivity of free space.
The potential at the center of Ring A due to Ring B (which has charge -q) is calculated considering the distance from the center of Ring B to the center of Ring A, which is √R2+d2:
VA due to B=14πϵ0⋅−q√R2+d2
The total potential at the center of Ring A is the sum of the potentials due to its own charge and the charge of Ring B:
Va=14πϵ0⋅qR−14πϵ0⋅q√R2+d2
Va=q4πϵ0(1R−1√R2+d2)
Using similar logic, the potential at the center of Ring B due to its own charge -q is:
Vb=14πϵ0⋅−qR
And the potential at the center of Ring B due to Ring A (which has charge +q) is:
VB due to A=14πϵ0⋅q√R2+d2
The total potential at the center of Ring B is:
Vb=−q4πϵ0R+q4πϵ0√R2+d2
Vb=q4πϵ0(1√R2+d2−1R)
The potential difference between the centers of the two rings is:
ΔV=Va−Vb
Substituting the expressions for Va and Vb:
ΔV=q4πϵ0(1R−1√R2+d2)−q4πϵ0(1√R2+d2−1R)
Combining the two terms gives:
ΔV=q4πϵ0(2R−2√R2+d2)
ΔV=q2πϵ0(1R−1√R2+d2)
Thus, the potential difference between the centers of the two rings is:
ΔV=q2πϵ0(1R−1√R2+d2)
Topper's Solved these Questions
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems2videos
ELECTROSTATICS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions2videos
ELECTROSTATICS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced107videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer1videos
MODERN PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is
AzeroBQ4πε0[1R−1√R2+d2]CQ4πε0d2)DQ2πε0[1R−1√R2+d2] - Question 2 - Select One
A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
Aλ4εoln0Bλ4π2ε0rCλ4πε0rDλ4πε0r2 - Question 3 - Select One
A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q(R>r0. The potential difference between the two is
AProportional to QBProportional to qCDependent on both Q and qDIndependent of both Q and q
Two identical thin rings, each of radius R, are coaxially placed a distance R apart. Q1 and Q2 are respectively the charges uniformly spread on the two rings. The work done in moving a charge q fróm the centre of one ring to that of the other is (√x−y)q(Q2−Q1)4√2πɛ0R. Find (x−y)
View SolutionA spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q (R > r). The potential difference between the two is
View SolutionTwo identical rings PandQ of radius 0.1m are mounted coaxially at a distance 0.5m apart. The charges on the two rings are 2μCand4μC, respectively. The work done in transferring a charge of 5μC from the center of P to that of Q is.
View SolutionTwo conducting rings P and Q of radius r and 3r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings a
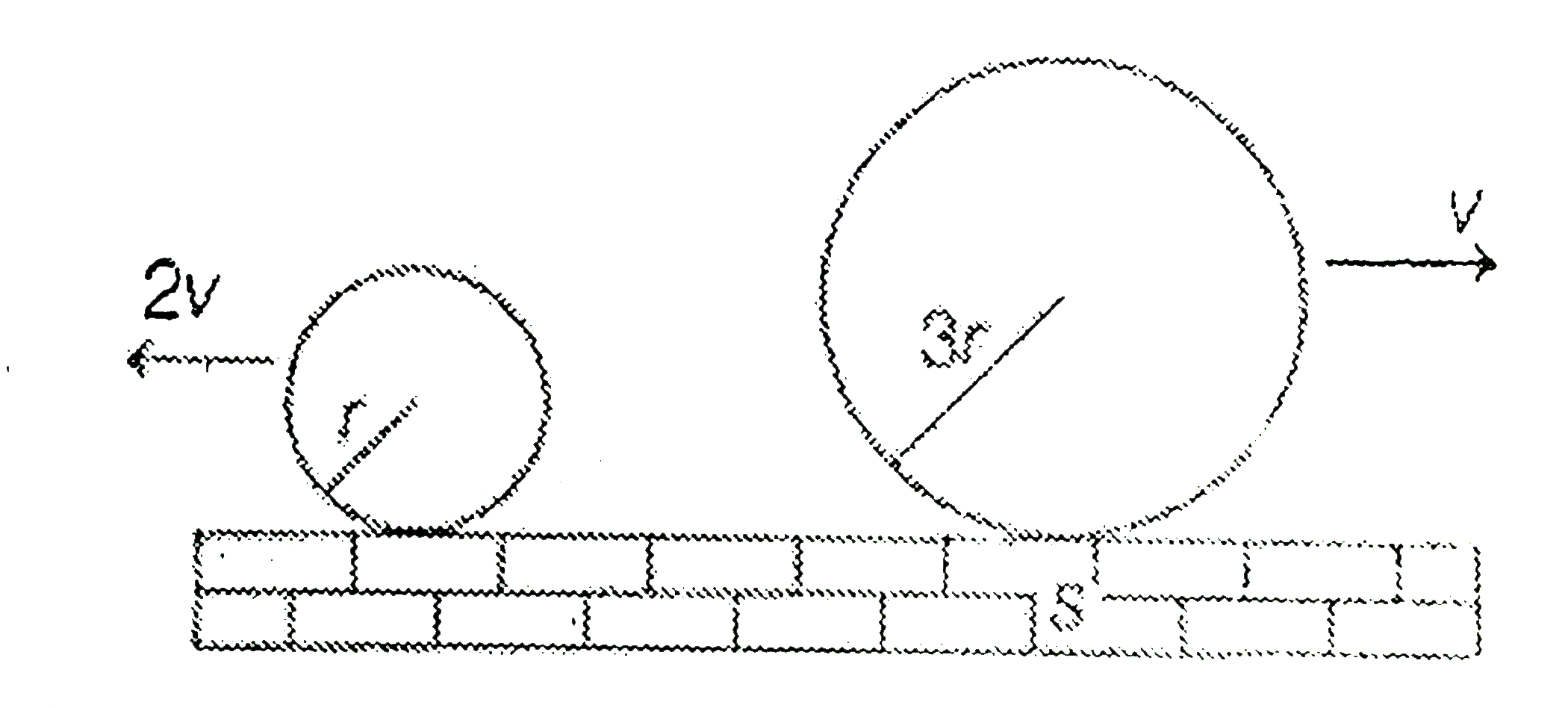 View Solution
View SolutionTwo metallic rings of radius R are rolling on a metallic rod. A magnetic field of magnitude B is applied in the region. The magnitude of potential difference between points A and C on the two rings (as shown) , will be
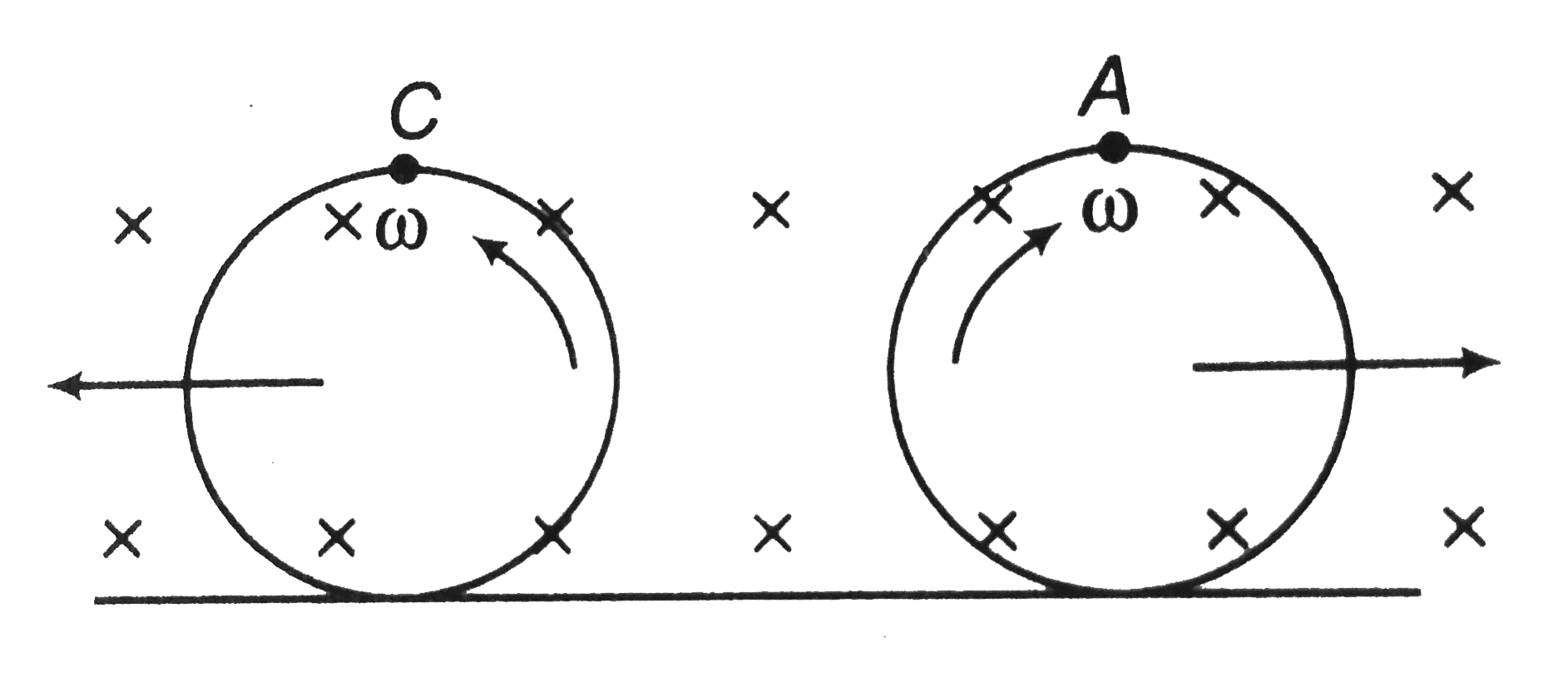 View Solution
View Solution

