Two transparent slabs have the same thickness as shown in figure. One in made of material A of refractive index 1.5. The other is made of two materilas B and C with thickness in the ratio 1:2. The refractive index of C is 1.6. If a monochromatic parallel beam passing through the slabs has the same number of wavelengths inside both, the refractive index of B is
1.1
1.2
1.3
1.4
The correct Answer is:c
Total number of waves =(1.5)tλ
(Total number of waves)=(optical path lengthwavelength)
For B and C:
Total number of waves =n0(t3)λ+1.6(2t3)λ
Equating (i) and (ii), we get
n0=1.3
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
A prism made of material with refractive index 1.6 has a prism angle of 9∘. Calculate the angle of deviation of the prism.
View SolutionThe ratio of the thickness of the strips of two transparent media A and B is 3:2 , if light takes the same time in passing through both of them , then what is the refractive index of B with respect to A ?
View Solution
Knowledge Check
The number of waves in a glass slab of thickness 4 cm is the same as in a water column of height 5 cm ,when the same monochromatic ray of light travels through them .what is the refractive index of water if the refractive index of glass is 53 ?
A1.25B1.5C1.33D1.75Two optical media of refractive indices n1 and n2 contain x and y waves of the same colour in the same thickness. Then their relative refractive index n1/n2
Ax−yBx/yC(y−x)/xDx/(y−x)A ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
A0.1 mB0.2 mC0.3 mD0.4 m
A light passes through glass slabv of refractive index 1.5 and thickness 2 mm. How much time ray will take to pass through the glass slab ?
View SolutionA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
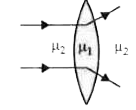
View SolutionA spot is placed on the bottom of a slab made of transperent material of refractive index 1.5. The spot is viewed vertically from the top when it seems to be raised by 2 cm. Then, the height of the slab is
View SolutionThere is a thin prism of angle 5∘ made of material having refractive index 1.6. There is another thin prism made of material of refractive index 1.8. These two prisms are combined in such a manner that they may produce dispersion without mean deviation. What should be the angle of second prism ?
View SolutionA concave lens of glass, refractive index 1.5, has both surface of same radius of curvature R. On immersion in a medium of refractive index 1.75, it will have as a
View Solution
