Two uniform boards, tied together with the help of a string, are balanced on a surface as shown in Fig.
The coefficient of static friction between boards and surface is 0.5. The minimum value of θ, for which this type of arrangement is possible is

30∘
45∘
37∘
it is not possible to have this type of balanced arrangement
The correct Answer is:B
For the equilibrium of the entire structure N1+N2=2Mg

Mg(l2cosθ)+N2×2x−Mg(l2cosθ+2x)=0
Given N2=Mg,N1=Mg
For individual boards, T1=f1,N2=Mg
and T1×lsinθ=Mg2tanθ
For safe equilibrium f1<fL=μsMg
Mg2tanθ=μsMg⇒tanθ>12μs⇒θ=45∘
So the minimum value of θ for this type of arrangement is 45∘
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
Knowledge Check
- Question 1 - Select One
The coefficient of static friction between two surfaces depend on
Anature of surfaceBthe shape of the surface in contactCthe area of contactDall of the above - Question 2 - Select One
The coefficient of friction between two surface is 0.2. The maximum angle of friction is
Asin−1(0.2)Bcos−1(0.2)Ctan−1(0.1)Dcot−1(5) - Question 3 - Select One or More
Two identical unifrom rods tied together with the help of a string are balanced as shown in the figure, then.

Choose the correct option(s).AThe minimum coefficient of frication for which the systeam will remain in equilibrium in the shown position is 23.BThe minimum coefficient of frication for which the systeam will remain in equilibrium in the shown position is 25.CIf the coefficient of frication is 0.5, then the system will remain in equilibrium in the shown position.DIf the coefficient of frication is 0.7, then the system will remain in equilibrium in the shown position.
Two identical unifrom rods tied together with the help of a string are balanced as shown in the figure, then.

Choose the correct option(s).View SolutionThe limiting value of static friction between two contact surfaces is
View SolutionWhat is the angle of friction, if the coefficient of friction between two surfaces is 0.25 ?
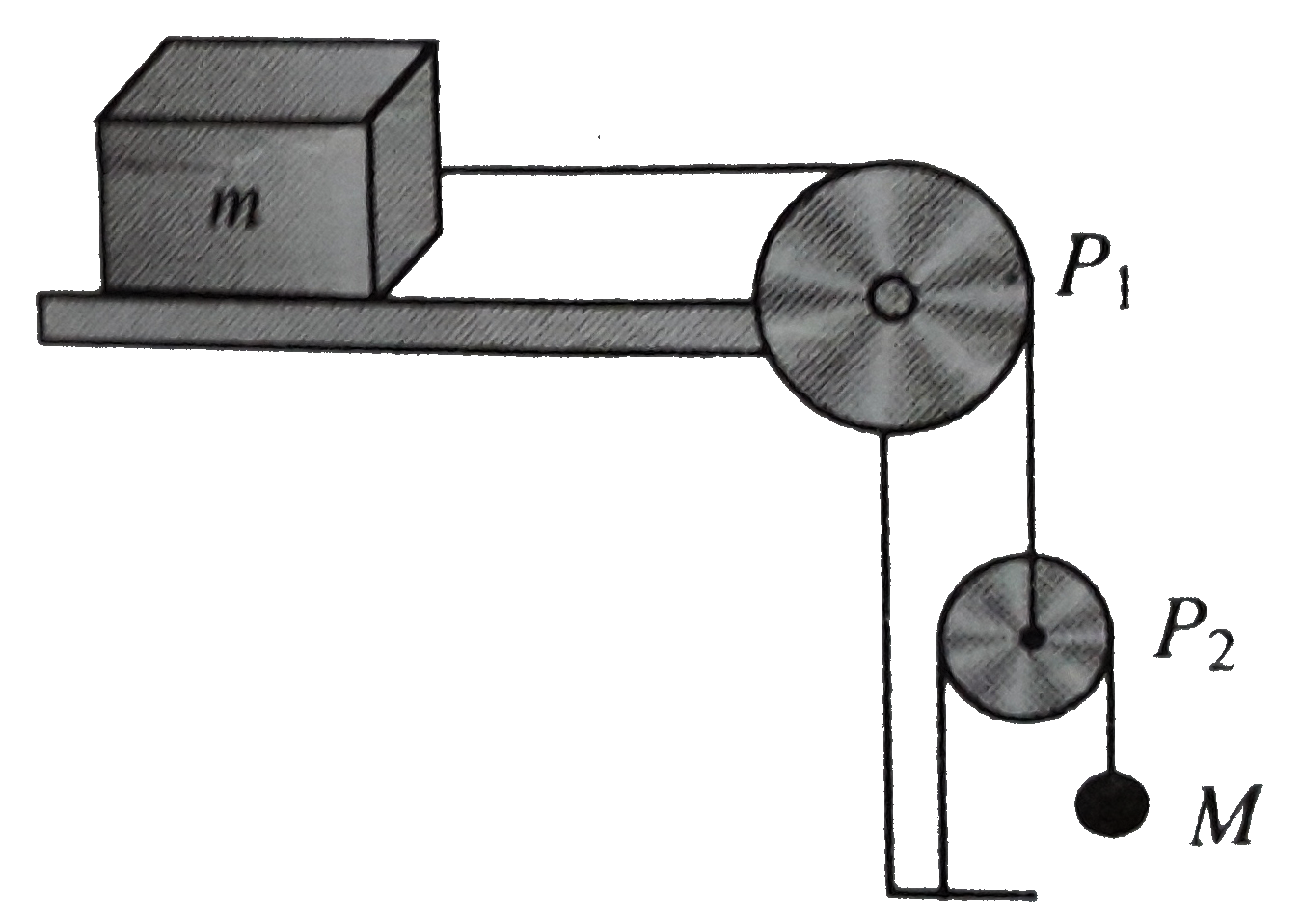
View SolutionIn the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μ the minimum value of M for which m is at rest is
 View Solution
View SolutionIn Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :
 View Solution
View Solution