Two uniform, thin identical rods each of mass M and length are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
The correct Answer is:B
To find the moment of inertia of the cross formed by two uniform, thin identical rods about an axis passing through their joint point and perpendicular to the plane of the cross, we can follow these steps:
Step 1: Identify the components
We have two identical rods, each with mass M and length l. They are positioned to form a cross, meaning they intersect at their midpoints.
Step 2: Moment of Inertia for a Single Rod
The moment of inertia I of a uniform rod about an axis passing through its center of mass and perpendicular to its length is given by the formula:
ICM=112Ml2
where M is the mass of the rod and l is its length.
Step 3: Calculate the Moment of Inertia for Each Rod
Since both rods are identical, the moment of inertia for each rod about its center of mass is:
ICM1=112Ml2(for Rod 1)
ICM2=112Ml2(for Rod 2)
Step 4: Total Moment of Inertia about the Joint Point
The total moment of inertia about the point where the two rods are joined (point O) can be calculated by adding the moment of inertia of both rods. Since the axis of rotation is through the joint point and perpendicular to the plane of the cross, we can directly add the two moments of inertia:
IO=ICM1+ICM2=112Ml2+112Ml2=212Ml2=16Ml2
Conclusion
Thus, the moment of inertia of the cross about the axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross is:
IO=16Ml2
Final Answer
The correct answer is Ml26.
---
We have two identical rods, each with mass M and length l. They are positioned to form a cross, meaning they intersect at their midpoints.
The moment of inertia I of a uniform rod about an axis passing through its center of mass and perpendicular to its length is given by the formula:
ICM=112Ml2
where M is the mass of the rod and l is its length.
Since both rods are identical, the moment of inertia for each rod about its center of mass is:
ICM1=112Ml2(for Rod 1)
ICM2=112Ml2(for Rod 2)
The total moment of inertia about the point where the two rods are joined (point O) can be calculated by adding the moment of inertia of both rods. Since the axis of rotation is through the joint point and perpendicular to the plane of the cross, we can directly add the two moments of inertia:
IO=ICM1+ICM2=112Ml2+112Ml2=212Ml2=16Ml2
Thus, the moment of inertia of the cross about the axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross is:
IO=16Ml2
The correct answer is Ml26.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Two rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure

View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionFour identical uniform thin rods, each of mass m and length l are joined to a common point O as shown in the figure. Moment of inertia of the system about an axis passing through O and lying in the plane of rods is
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

View SolutionThree identical rods each of mass M, length l are joined to form an equilateral ΔABC . Find the Moment of Inertia about BC as shown.
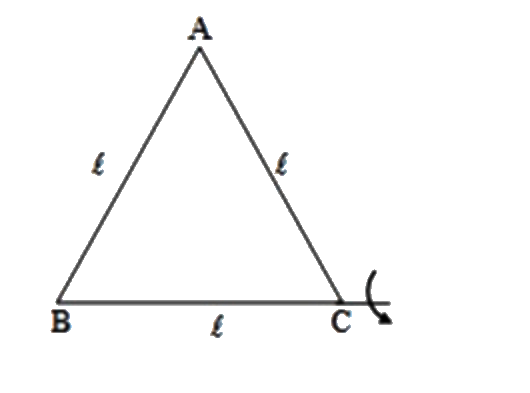
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionFour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View Solution
