Two vibrating bodies have frequencies 10 Hz and 12 Hz. They start oscillating in the sáme phase. In 3 seconds how many time they will be (i) in the same phase and (ii) in the opposite phase ?
To solve the problem, we need to determine how many times two vibrating bodies with frequencies of 10 Hz and 12 Hz will be in the same phase and in the opposite phase within a time frame of 3 seconds.
Step 1: Determine the period of each vibrating body.
The period T of a vibrating body is the reciprocal of its frequency f:
T=1f
For the first body (10 Hz):
T1=110=0.1 seconds
For the second body (12 Hz):
T2=112≈0.0833 seconds
Step 2: Calculate the least common multiple (LCM) of the periods.
To find when both bodies will be in the same phase, we need to calculate the LCM of their periods T1 and T2.
Convert the periods to a common unit (in seconds):
- T1=0.1 seconds
- T2≈0.0833 seconds
To find the LCM, we can convert these to fractions:
T1=110andT2=112
The LCM of the denominators (10 and 12) is 60. Therefore:
LCM(T1,T2)=1GCD(10,12)=6010×12=60120=12 seconds
Step 3: Determine how many times they are in the same phase in 3 seconds.
To find how many times they are in the same phase, we divide the total time by the LCM:
Number of times in the same phase=3 secondsLCM(T1,T2)
=312=3×2=6
Step 4: Determine how many times they are in the opposite phase.
Two bodies are in the opposite phase when they are T12 and T22 apart. Since they are in the opposite phase every half period of their LCM, we can calculate:
Number of times in the opposite phase=3 seconds14=3×4=12
Final Answer:
(i) They will be in the same phase 6 times in 3 seconds.
(ii) They will be in the opposite phase 12 times in 3 seconds.
T=1f
T1=110=0.1 seconds
T2=112≈0.0833 seconds
- T1=0.1 seconds
- T2≈0.0833 seconds
T1=110andT2=112
LCM(T1,T2)=1GCD(10,12)=6010×12=60120=12 seconds
Number of times in the same phase=3 secondsLCM(T1,T2)
=312=3×2=6
Number of times in the opposite phase=3 seconds14=3×4=12
(i) They will be in the same phase 6 times in 3 seconds.
(ii) They will be in the opposite phase 12 times in 3 seconds.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS WITH ANSWER20videos
OSCILLATIONS
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS3videos
OSCILLATIONS
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS12videos
PROPERTIES OF MATTER
Similar Questions
Two pendulum of time periods 3 s and 7 s respectively start oscillating simultaneously from two opposite extreme positions. After how much time they will be in same phase?
View SolutionThe rope shown at an instant is carrying a wave travelling towards right, created by a source vibrating at a frequency n . Consider the following statements
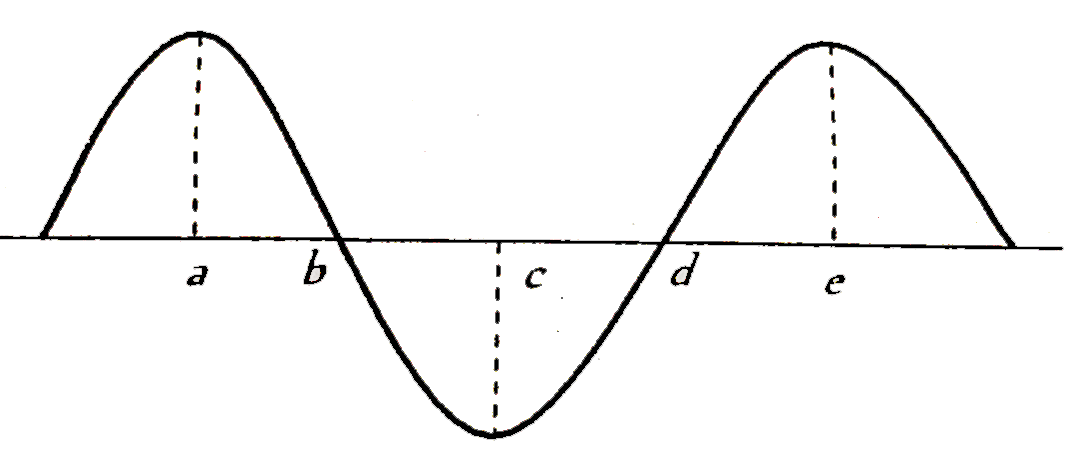
I. The speed of the wave is 4n×ab
II. The medium at a will be in the same phase as d after 43ns
III. The phase difference between b and e is 3π2
Which of these statements are correctView SolutionTwo pendulums X and Y of time periods 4s and 4.2s are made to vibrate simultaneously. They are initially in same phase. After how many vibration of X, they will be in the same phase again ?
View SolutionTwo sinusoidal wave having the same frequency and travelling in the same direction are combined. What is the amplitude of the resultant motion if their amplitudes are 3cm and 4cm and they differ in phase by π/2 radian?
View SolutionTwo tunig forks of frequency 250Hz and 256Hz produce beats. If a maximum is observed just now, after how much time the next maximum is observed at the same place?
View SolutionTwo waves, each having a frequency of 100 Hz and a wavelength of 2.0 cm, are travelling in the same direction on a string. What is the phase difference between the waves (a) if the second wave was produced 0.015 s later than the first one at the same place, (b) if the two waves were produced at the same instant but the first one was produced a distance 4.0 cm behind the second one ? (c) If each of the waves has an amplitude of 2.0 mm, what would be the amplitudes of the resultant waves in part (a) and (b) ?
View SolutionAssertion : When two vibrating tuning forks having frequencies 256Hz and 512Hz are held near each other , beats can not be heard .
Reason : The principle of superposition is valid only if the frequencies of the oscillators are nearly equal.View SolutionTwo waves, each having a frequency of 100 Hz and a wavelength of 2.0 cm, are travelling in the same direction on a string. What is the phase difference between the waves if the second wave was produced 0.015 s later than the first one at the same place,
View SolutionTwo simple pendulums have time period 4s and 5s respectively. If they started simultaneously from the mean position in the same direction, then the phase difference between them by the time the larger one completes one oscillation is
View Solutiontwo partical excuting SHM with same frequency and amplitudes Aand2A on same straight line with same mean position cross each other in opposite direction at a distance A/3 from mean possion. Find the phase difference in the two SHM s.
View Solution

