Two wires ACandBC are tied at C of small sphere of mass 5kg which revolves at a constant speed v in the horizontal circle of radius 1.6m Find the maximum value of v
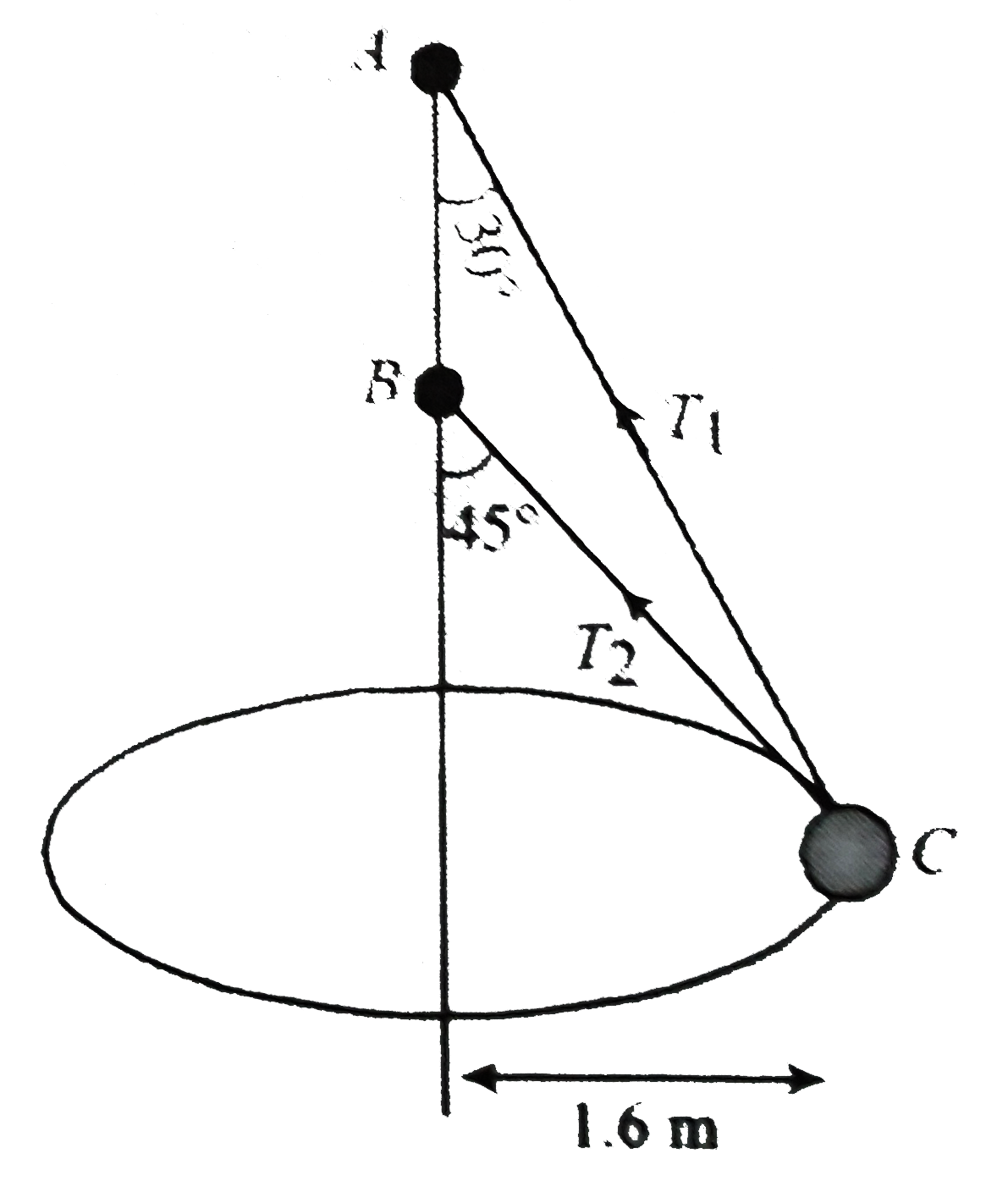
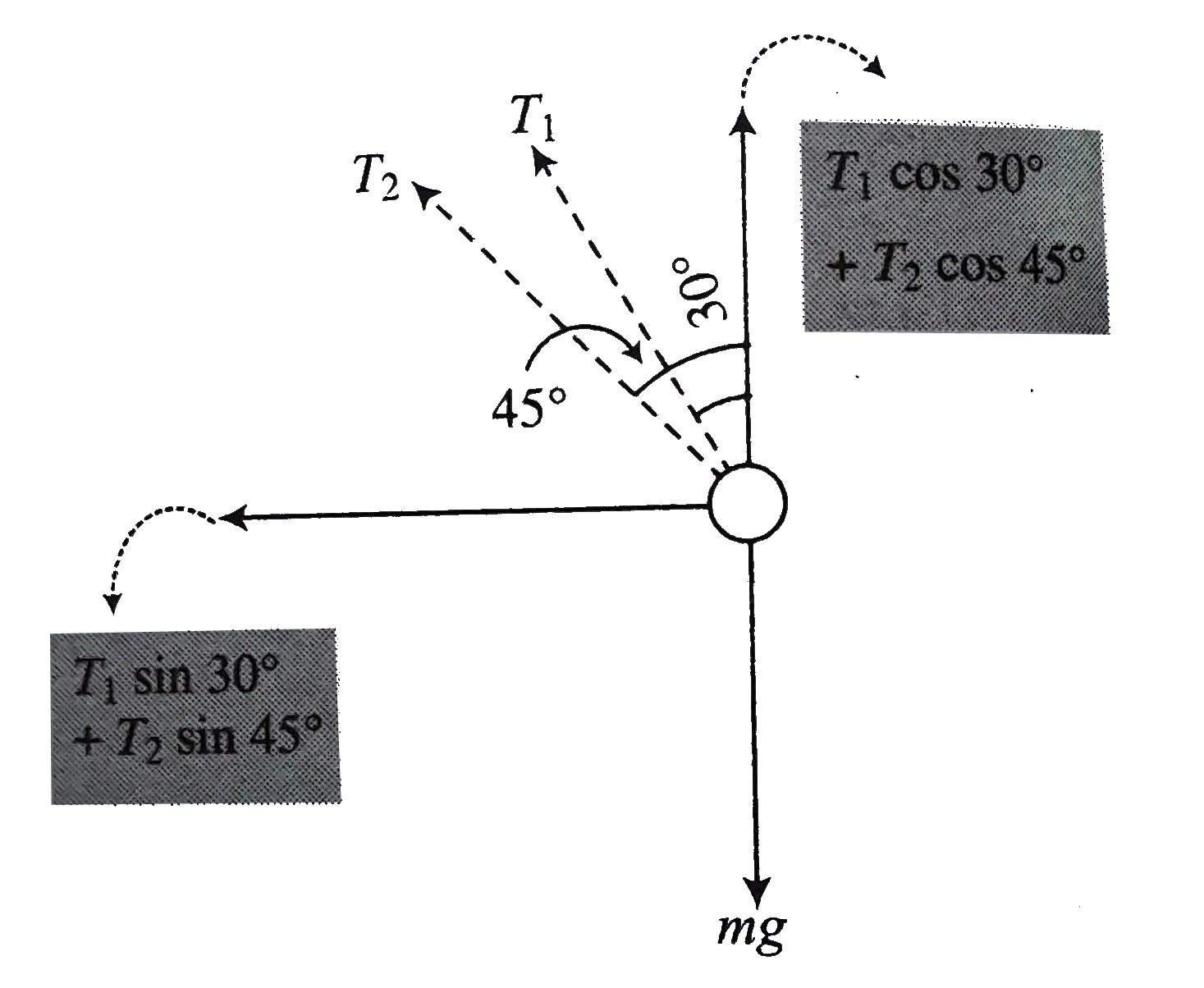
From force diagram shown in Fig
T1cos30∘+T2cos45∘=mg….(i)
T1sin30∘+T2sin45∘=mv2r….(ii)
After solving Eqs. (i) and (ii)
T1=mg−nv2r(√3−1)2
But T1>0,=mg−nv2r√3−12>0⇒mg>mv2r<<br>rArr v ltsqrt (rg)<br>v_(max) = sqrt(rg) = sqrt(1.6 xx 9.8 ) = 3.96 ms^(-1)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
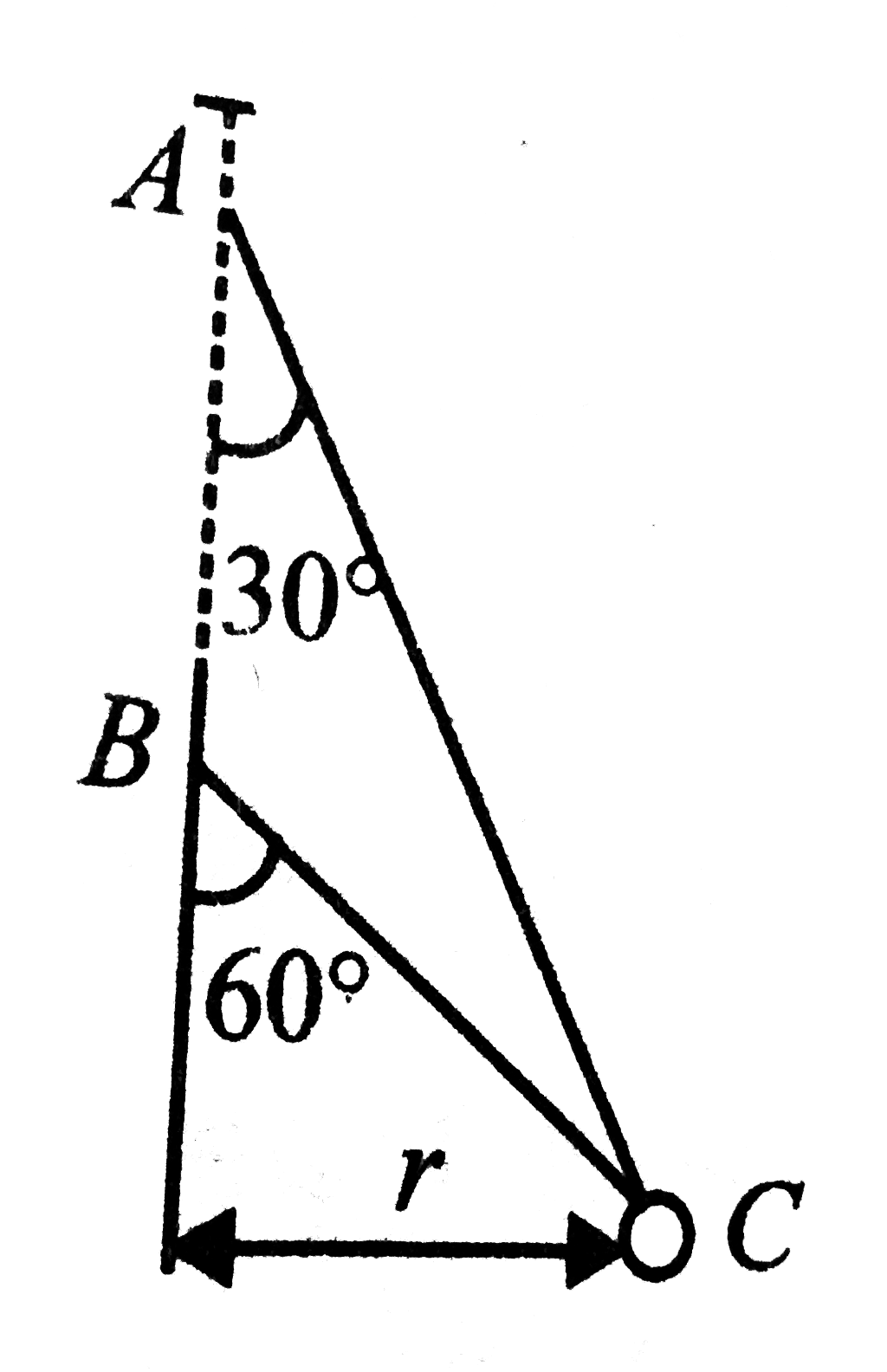
A single wire ACB passes through a smooth ring at C which revolves at a constant speed in the horizontal circle of radius r as shown in the figure. The speed of revolution is √yrg6. Find y.
'(##CEN_KSR_PHY_JEE_C07_015_Q09##)'View SolutionA single wire ACB passes through a smooth ring at C when revolves at a constant speed in the horizontal circle of radius r=6.4m as shown in the figure. Find the speed (in m/s) of revolution of the ring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two wires Ac an Bc are tied at C of small sphere of mass 5 kg Which reolves at ta constant speed v in the horzontal circle of radius of 1.6 m. The minimum value of v is
 A3.01m/sB4.01m/sC8.2m/sD3.96m/s
A3.01m/sB4.01m/sC8.2m/sD3.96m/s - Question 2 - Select One
Two wires AC and BC are tied at C of a small sphere of mass 5kg, wheich revolves at a constant speed v in the horizontal speed v in the horizontal circle of radius 1.6m. Find the minimum value of v
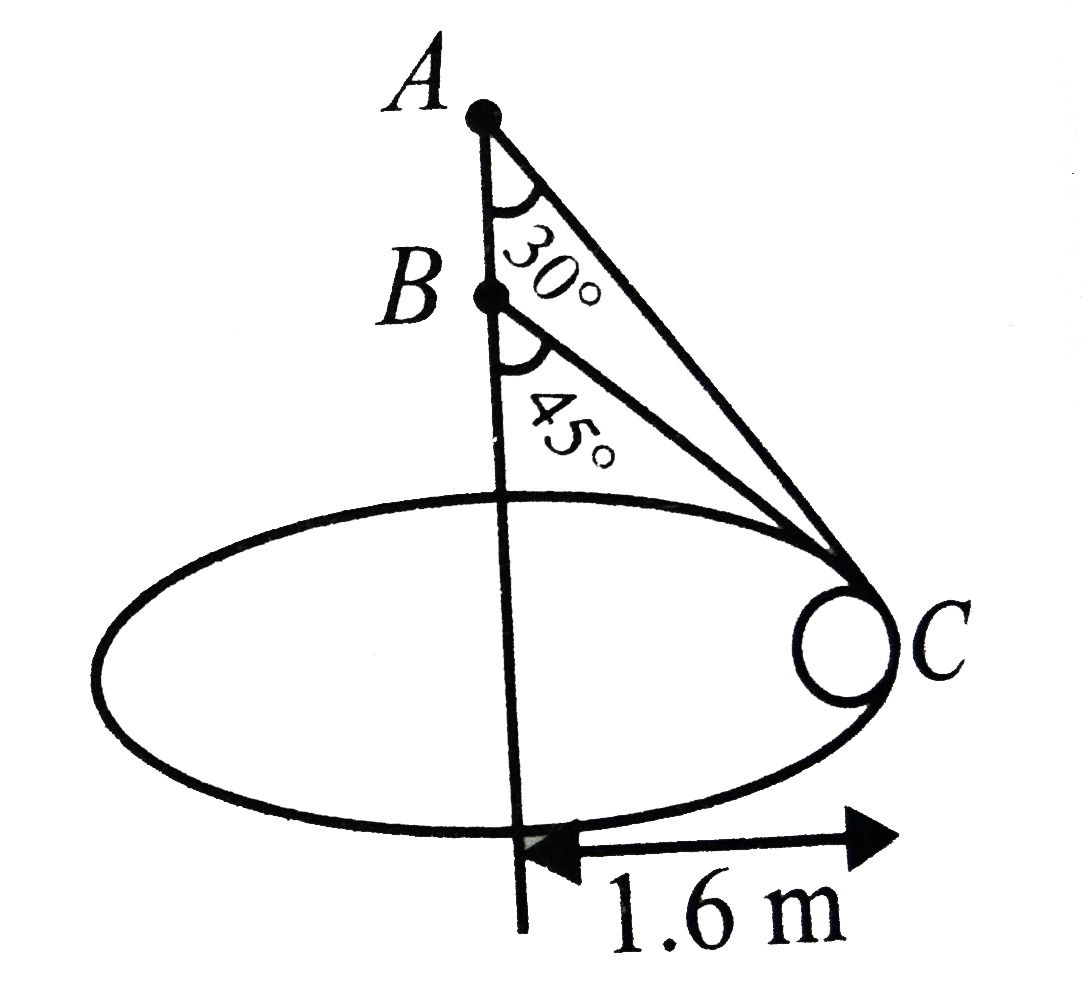 A4ms−1B2ms−1C2.5ms−1Dnone of these
A4ms−1B2ms−1C2.5ms−1Dnone of these - Question 3 - Select One
A single wire ACB passes through a smooth ring at C which revolves at a constant speed in the horizontal circle of radius r as shown in the fig. the speed of revolution is
 A√rgB√2rgC2√2rgD2√rg
A√rgB√2rgC2√2rgD2√rg
Consider a vehicle taking turn on the horizontal curve with speed v. If the distance between wheels is 2m, height of center of mass above road is 1m and radius of circle is 57.6m, find the maximum value of v for no overturning.
View SolutionA body of mass 10 kg moves with a constant speed v of 2 ms−1 along a circular path of radius 8 m. The power produced by the body will be
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionThe breaking tension of a string is 10 N. A particle of mass 0.1 kg tied to it is rotated along a horizontal circle of radius 0.5 meter. The maximum speed with which the particle can be rotated without breaking the string is
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 View Solution
View Solution

